O tempo (em horas) necessário para reparar uma máquina é uma variável aleatória Exponencialmente distribu��da com parâmetro .
(d) Suponha agora que a distribuição do tempo () de reparo não seja mais Exponencial, mas que possa ser modelada por uma Normal com os mesmos parâmetros Média e Variância da Exponencial . Nesta nova condição calcule , Mediana() e DIQ().
Passo 1
Letra d)
Vamos começar calculando a média e variância da nossa Exponencial, que são dadas pelas fórmulas:
Como nosso :
E ele diz pra gente que segue uma Normal com a mesma média e variância de . Então:
Agora temos que calcular! Como é uma Normal, bora padronizar issaê:
Quando temos um valor negativo ali dentro, basta invertermos o sinal de ou e tirar o negativo, desse jeito aqui:
E agora já temos nossa probabilidade no formato certinho pra procurar o valor dela na tabela da Normal:
Passo 2
E pra finalizar ele tá pedindo pra gente de uma Normal! Como fazemos isso?
Olha o pulo do gato agora!

A tabela da Normal nada mais fornece valores de probabilidades até certo ponto, lembra? Por exemplo:
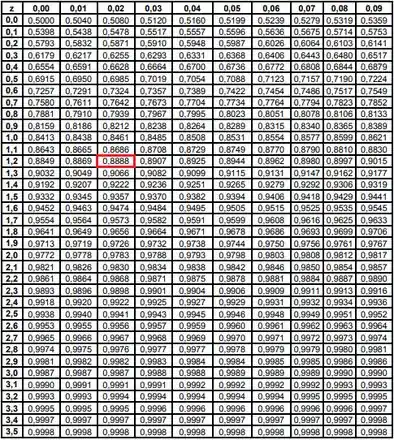
Se eu quisesse saber a partir de qual valor nós temos 0,8888 dos nossos dados, eu veria qual o associado à probabilidade 0,8888 no corpo da tabela, que é 1,22.
E quando falamos de medianas e quartis, é justamente isso que a gente quer saber, certo? Em qual valor nós temos 0,25, 0,50 e 0,75 dos nossos dados! Vamos procurar essas probabilidades no corpo da tabela e ver quais os associados a elas:
Peraê, da onde veio esse pra 0,25? Nossa tabela começa a partir de 0,5, então não temos 0,25 nela. Por isso temos que procurar a probabilidade complementar de 0,25, ou seja, 0,75, e colocar o sinal de menos na frente do associado a ela, beleza?
Acabou??? NÃO!!! Muita calma nessa hora!!! Não podemos esquecer que a tabela da Normal é associada à Normal Padrão, ou seja, aquela que tem média 0 e desvio padrão 1! E na nossa questão nossa Normal tem média 2 e desvio padrão 2 também, lembra?
Então esses que a gente achou são os quartis e a mediana de uma Normal Padrão. Pra adaptar esses caras à nossa Normal vamos ter que: multiplicar cada pela média e somar o desvio-padrão! Assim vamos “compensar” as diferenças do gráfico da Normal Padrão e da nossa Normal. Se liga:
E nossa então vai ser:
UFA!!! Foi!
Resposta
Letra d)