14) Um dado de 6 faces, viciado, possui probabilidade de ocorrência de cada face proporcional ao número de pontos desta. Lança-se este dado. Caso a face apresente um número maior que 3, sorteia-se um número entre 1 e 9 uniformemente. Caso a face apresente um número menor que 4, sorteia-se um número entre 1 e 5 uniformemente. Qual é a probabilidade de o número sorteado ser par?
a)
b)
c)
d)
e)
Passo 1
Faaaaala galera! Quem tá animado pra descobrir o mistério desse dado maluco?
Essa questão traz um problema bem interessante. Imagina que você tem um dado que quando é lançado, a probabilidade de sair um número qualquer é diretamente proporcional a esse número. Tipo assim, a probabilidade de sair o número 5, por exemplo é:
O mesmo vale para os outros números do dado (1, 2, 3, 4 e 6).
Só que esse dado é só a primeira parte da brincadeira. Depois que ele for lançado, se o resultado for 4, 5 ou 6 será feito um sorteio de 1 a 9, com resultados equiprováveis. Se o resultado do dado for 1,2 ou 3 será feito um sorteio de 1 a 5, também equiprovável.
A pergunta do milhão é: Qual a probabilidade de, no final de tudo, ser sorteado um número par?
Passo 2
Bom, agora que a gente sacou a ideia desse sorteio maluco, precisamos ir por partes. Primeiro, bora descobrir a probabilidade de, no lançamento do dado, termos ou (onde é o resultado do lançamento).
Pela proporcionalidade do dado viciado, temos:
Ok, mas e quem é esse ?

O é justamente a constante de proporcionalidade. Para descobrir o seu valor, podemos usar um resultado conhecido. Pois sabemos que a probabilidade de no lançamento de um dado qualquer, viciado ou não, sair ou é , ou seja, , porque não tem como sair um número diferente desses. Daí:
Logo:
Perfeito! Então a probabilidade de termos é:
Além disso, usando a complementaridade da probabilidade, vem que:
Boa, agora vamos analisar o resultado do sorteio.
Passo 3
Se no lançamento do dado a gente tiver , será feito um sorteio equiprovável entre números. A probabilidade de sair um número par é de . Porque há números pares dentre os a serem sorteados.
Já se no lançamento do dado a gente tiver , será feito um sorteio dentre 5 números. A probabilidade de sair um número par é de pois há pares dentre os 5 números.
Excelente pessoal! Agora a gente pode montar nossa árvore de probabilidade pra encerrar a questão com classe hahaha.
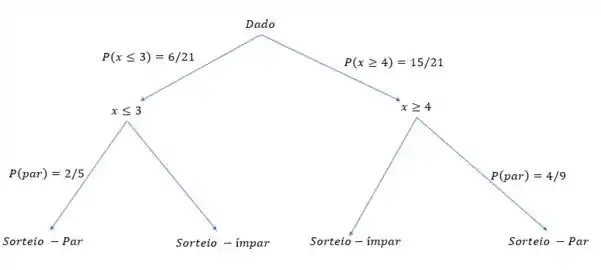
Beleza! Como a gente quer saber a probabilidade de ser sorteado um número par, basta somarmos os ramos que resultam em um sorteio par. Logo:
Por fim, finalmente chegamos que:
Aeee, conseguimos!!! Vocês entenderam bem?
Bora pra próxima!
Resposta
Letra C: