Para dois eventos A e B, num mesmo espaço amostral, verifique, através de um diagrama, que é sempre possível escrever o evento A como sendo e que, portanto, vale .
Passo 1
Primeiro, antes de qualquer coisa vamos desenhar o nosso espaço amostral e seus respectivos subconjuntos (eventos).
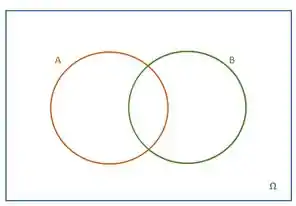
Feito isso, vamos começar a analisar a expressão dada:
A melhor idéia aqui é analisar por partes. Vamos dividir?
(i)
(ii)
Passo 2
Analisando (i) :
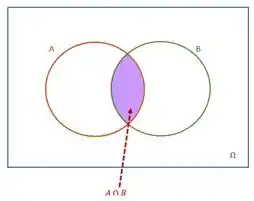
Passo 3
Analisando (ii)
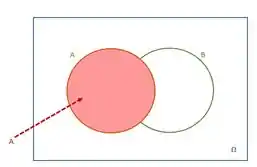
A
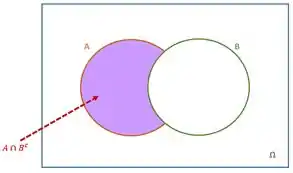
Passo 4
Fazendo
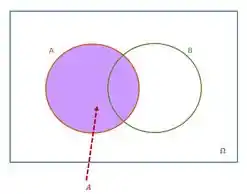
Ou seja, através do diagrama verificamos que A= .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Amostras de uma peça de alumínio fundido são classificadas com base no acabamento (em micropolegadas) da superfície e no acabamento de borda. Os resultados de 100 peças são resumidos a seguir:Seja A o
14. Que suposições devem ser feitas para que os resultados dos experimentos abaixo possam ser considerados equiprováveis?(b)Opinião de moradores de uma cidade sobre um projeto governamental.
Um lote contém peças pesando 5, 10, 15, ..., 50 gramas. Admitamos que ao menos duas peças de cada peso sejam encontradas no lote. Duas peças são retiradas do lote. Seja X o peso da primeira peça escol
Em replicação controlada, células são replicadas em um período de dois dias. DNA recém-sintetizado não pode ser replicado novamente até que a mitose esteja completa. Dois mecanismos de controle foram
O tempo de enchimento de um reator é medido em minutos (e frações de minutos). seja o espaço amostral por números reais e positivos. Defina os eventos A e B como segue: A = { x | x72.5 } e B = { x | x