Sendo A e B dois eventos em um mesmo espaço amostral, “traduza” para a linguagem da Teoria dos Conjuntos, as seguintes situações:
a) Pelo menos um dos eventos ocorre.
b) O evento A ocorre mas B não.
c) Nenhum deles ocorre.
Passo 1
Vamos lá: A e B são eventos ou seja, subconjuntos do meu espaço amostral.
Como o enunciado não informou se eles possuem interseção ou não, vamos considerar que tem. (Note que não tem problema considerar que , pois este é o caso mais abrangente.)O diagrama de Venn ficaria assim:
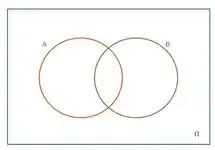
Passo 2
a) Pelo menos um evento ocorre.
Vamos interpretar essa frase: Se pelo menos um evento ocorre podemos dizer que ou apenas UM evento ocorre (ou A ou B) ou AMBOS ocorrem. Olhe na figura abaixo:
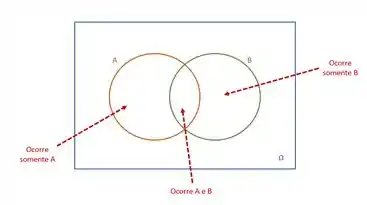
Note que a união desses três subconjuntos é exatamente .
Obs.: É bem comum, ao ler o “pelo menos um evento ocorre” pensar no espaço amostral (conjunto universo) menos o contrário do enunciado. Como assim?
Ele não pediu pelo menos um dos eventos ocorra? O contrário disso, o complementar, é que nenhum evento ocorra concordam?
Escrevendo “nenhum evento ocorra”:
Então escreveríamos:
Passo 3
b) O evento A ocorre mas B não.
Se o evento A ocorre mas o B não, podemos afirmar que neste caso a interseção de A com B (não irá ocorrer.
Na figura, a área preenchida será a desejada:
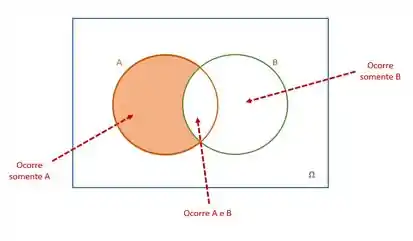
Essa área pode ser escrita como: ou .
Passo 4
c) Nenhum deles ocorre.
Se nenhum deles ocorre, note que teremos exatamente o oposto da letra (a), ou seja, o complementar da mesma.
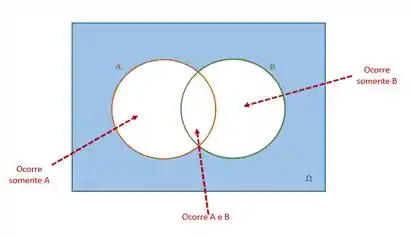
Assim, nenhum deles ocorre quando em .
Resposta
a) ou
ou
c)