Em uma pesquisa de mercado foram entrevistadas várias pessoas acerca de suas preferências em relação a três produtos, A, B e C. Os resultados da pesquisa indicaram que:
- 210 pessoas compraram o produto A
- 210 pessoas compraram o produto B
- 250 pessoas compraram o produto C
- 20 pessoas compraram os três produtos
- 100 pessoas não compraram nenhum dos três produtos
- 60 pessoas compraram os produtos A e B
- 70 pessoas compram os produtos A e C
- 50 pessoas compraram o conjunto B e C
Quantas pessoas foram entrevistadas?
Passo 1
Vaamos lá! Esse é um problema clássico que envolve conjuntos e probabilidade. Temos três conjuntos, que possuem (ou não) interseção.
O primeiro passo é desenha-los e entender bem o que cada região significa
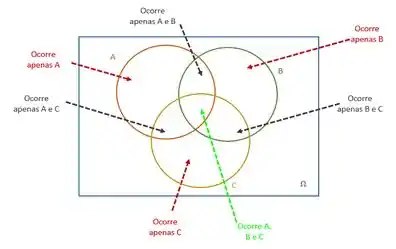
Passo 2
Agora que cada região está bem definida, vamos começar a completar o conjunto com os dados do enunciado. Existe uma ordem que é melhor para completar e torna todo o processo mais fácil.
1º Completar a região da interseção dos três conjuntos/eventos.
“20 pessoas compraram os três produtos”
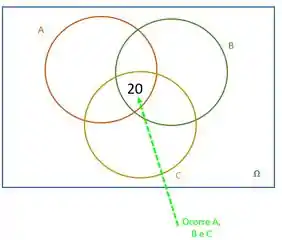
2º Completar as regiões das interseções duas a duas, tomando cuidado de não esquecer do valor já adicionado. Ou seja, pelo enunciado tempos:
60 pessoas compraram os produtos A e B Atenção! Está incluso nessas 60 pessoas as 20 pessoas que compraram A, B e C. Para saber quem comprou APENAS A e B devemos subtrair: 60-20 = 40 pessoas.
70 pessoas compram os produtos A e C Mesmo pensamento! Quem comprou APENAS A e C foram: 70-20 = 50 pessoas.
50 pessoas compraram o conjunto B e C Mesmo pensamento! Quem comprou APENAS B e C foram: 50-20 = 30 pessoas.
Então o diagrama vai ficar:
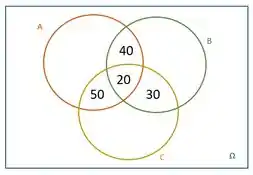
3º Completas as regiões que representam as pessoas que compraram apenas UM produto. Ou seja, compraram ou A ou B ou C.
A ideia é a mesma das regiões de interseção dois a dois. Devemos tomar cuidado pois o valor do enunciado não será o mesmo que escreveremos nessas regiões. Devemos subtrair dos valores já existentes ali.
Ficou confuso? Vamos pro diagrama!
“210 pessoas compraram o produto A”
“210 pessoas compraram o produto B”
“250 pessoas compraram o produto C”
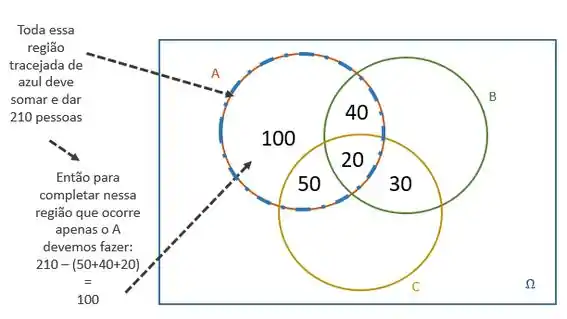
Seguindo o mesmo raciocínio para as outras regiões (B e C) teremos:
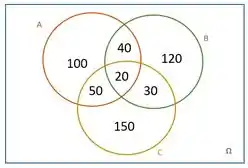
4º Completar com os elementos que não pertecem a nenhum desses conjuntos.
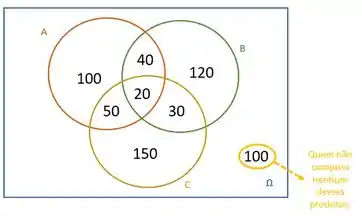
Passo 3
O número total de entrevistados é a soma de cada região:
Resposta
610 pessoas