Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Análise de Malha

Ver Teoria
Exercício 12345678910

Enunciado

Calcule as correntes de malha i 1 e i 2 na figura abaixo:

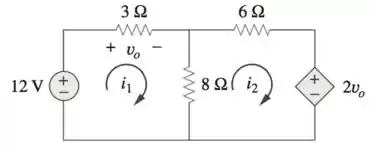
Passo 1

Vamos analisar a primeira malha:

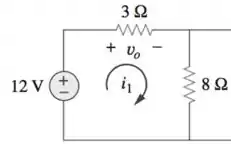
Temos que escrever as polaridades das quedas de tensão nos resistores, lembrando que como no resistor de 8Ω nós temos duas correntes passando por ele ( i 1   e   i 2 ) , temos que considerar essas duas quedas na equação da primeira malha:

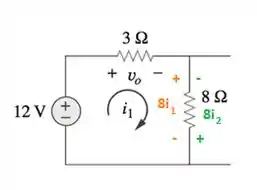
Logo, podemos escrever a equação da malha como:

- 12 + 3   i 1 + 8   i 1 - 8 i 2 = 0

Passo 2

Analisando a segunda malha:

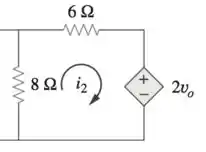
Temos que escrever as polaridades das quedas de tensão nos resistores, lembrando que como no resistor de 8Ω nós temos duas correntes passando por ele ( i 1   e   i 2 ) , temos que considerar essas duas quedas na equação da segunda malha:

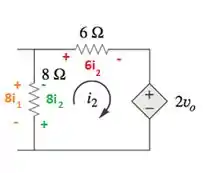
Logo, podemos escrever a equação da malha como:

8 i 2 - 8 i 1 + 6 i 2 + 2 v 0 = 0

Passo 3

Reunindo as equações de malha segundo a LTK, temos:

- 12 + 3 i 1 + 8 i 1 - i 2 = 0 8 i 2 - i 1 + 6 i 2 + 2 v 0 = 0

Como:

v 0 = 3 i 1

Substituindo:

11 i 1 - 8 i 2 = 12 - 2 i 1 + 14 i 2 = 0

Passo 4

Agora, precisamos resolver esse sistema. Vamos fazer assim:

Primeiro, vamos isolar i 2 na segunda equação:

i 2 = i 1 7

Substituindo na primeira:

11 i 1 - 8 i 1 7 = 12

i 1 = 1,22   A

Portanto, temos que:

i 2 = 1,22 7 = 0,17   A

Resposta

i 1 = 1,22   A

i 2 = 0,17   A

Exercícios de Livros Relacionados

Usando a análise de malhas. calcule v1.
Selecione a árvore do resistor de 4 Ω e do resistor de 2 Ω com a tensão v 1 e use o método de conjunto de corte para calcular v .
Resolva o Problema 4.13 usando o método das correntes de malha.
a) Use o método das correntes de malha para determinar quais fontes no circuito da Figura P4.48 estão fornecendo potência.b) Determine a potência total dissipada no circuito.
Resolva o Problema 4.27 usando o método das correntes de malha.