Determine , e no circuito da figura abaixo:
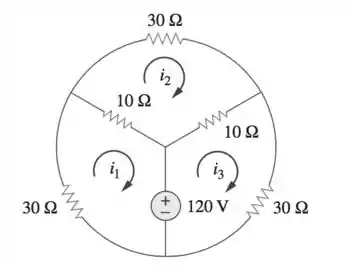
Passo 1
Primeira coisa a se fazer é LTK em cada malha, formando, assim, 3 equações:
Simplificando:
Passo 2
Isolando e das equações e :
Passo 3
Substituindo as equações do passo anterior em :
Passo 4
Substituindo o valor encontrado de nas equações e :
Resposta
Portanto,
Exercícios de Livros Relacionados
Usando a análise de malhas. calcule v1.
Selecione a árvore do resistor de 4 Ω e do resistor de 2 Ω com a tensão v 1 e use o método de conjunto de corte para calcular v .
Resolva o Problema 4.13 usando o método das correntes de malha.
a) Use o método das correntes de malha para determinar quais fontes no circuito da Figura P4.48 estão fornecendo potência.b) Determine a potência total dissipada no circuito.
Resolva o Problema 4.27 usando o método das correntes de malha.