Usando a abordagem da supermalha, calcule a corrente através de cada elemento do circuito:
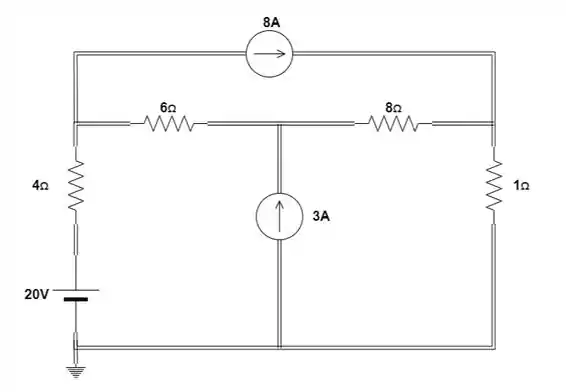
Passo 1
Vamos definir as correntes que percorrem as malhas:
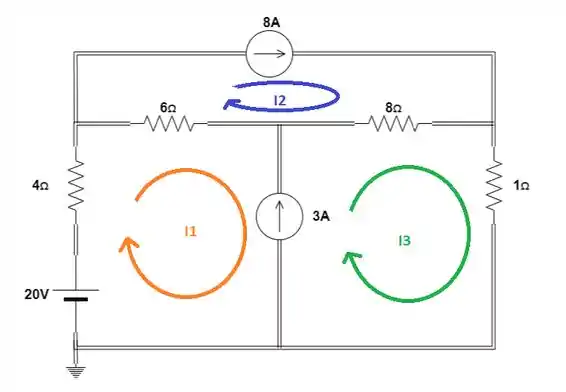
Passo 2
Agora vamos marcar as polaridades das quedas de tensão nos resistores.
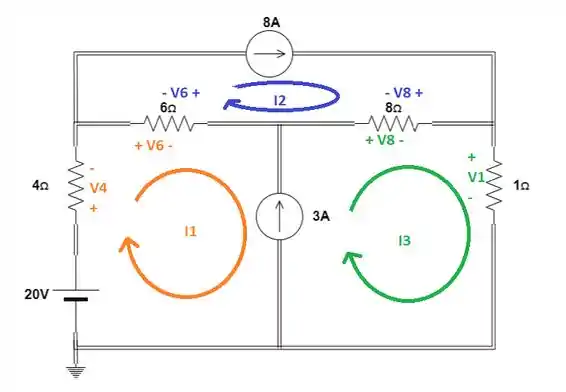
Passo 3
Podemos verificar através das fontes de corrente que:
Vamos escrever a equação das malhas para a malha que só possui resistores e nenhuma fonte de corrente:
Passo 4
Vamos substituir a corrente por 8A e :
Assim, encontramos que:
Então:
Resposta
As correntes são:
Exercícios de Livros Relacionados
Usando a análise de malhas. calcule v1.
Selecione a árvore do resistor de 4 Ω e do resistor de 2 Ω com a tensão v 1 e use o método de conjunto de corte para calcular v .
Resolva o Problema 4.13 usando o método das correntes de malha.
a) Use o método das correntes de malha para determinar quais fontes no circuito da Figura P4.48 estão fornecendo potência.b) Determine a potência total dissipada no circuito.
Resolva o Problema 4.27 usando o método das correntes de malha.