Usando a análise de malhas, calcule e no circuito abaixo, se:
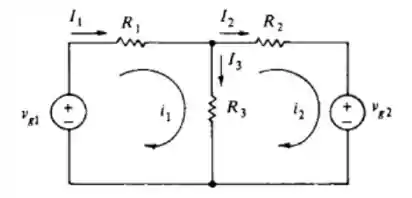
Passo 1
Vamos começar fazendo um LKT na malha 1 e 2 para achar e :
LKT na malha 1:
LKC na malha 2:
Passo 2
Como nós temos duas equações e duas incógnitas, podemos fazer um sistema e achar nossos resultados:
Multiplicando a primeira equação por e a segunda por ,
Somando as duas, chegamos em
Substituindo em qualquer uma das equações a gente acha o :
Resposta
Exercícios de Livros Relacionados
Usando a análise de malhas. calcule v1.
Selecione a árvore do resistor de 4 Ω e do resistor de 2 Ω com a tensão v 1 e use o método de conjunto de corte para calcular v .
Resolva o Problema 4.13 usando o método das correntes de malha.
a) Use o método das correntes de malha para determinar quais fontes no circuito da Figura P4.48 estão fornecendo potência.b) Determine a potência total dissipada no circuito.
Resolva o Problema 4.27 usando o método das correntes de malha.