Usando a abordagem geral para o método das malhas, determine a corrente através de cada resistor da figura:
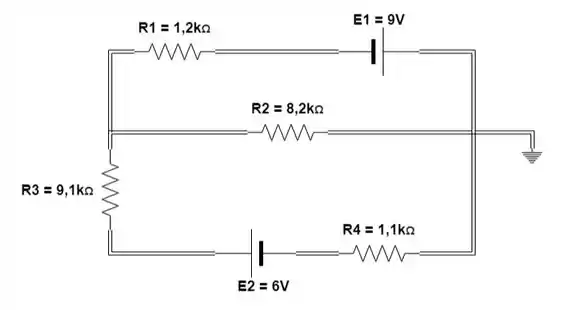
Passo 1
Primeiro devemos desenhar o sentido das correntes em cada malha e nomear cada uma delas
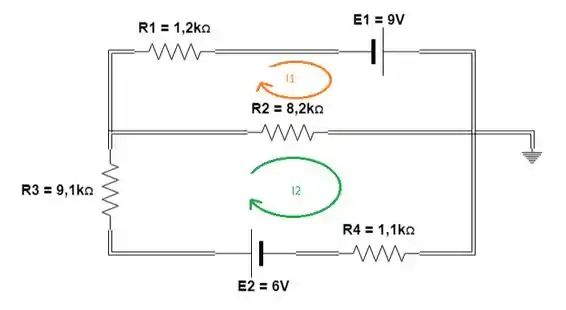
Passo 2
Agora vamos marcar as polaridades das quedas de tensão produzidas em cada resistor pelas correntes que atravessam eles:
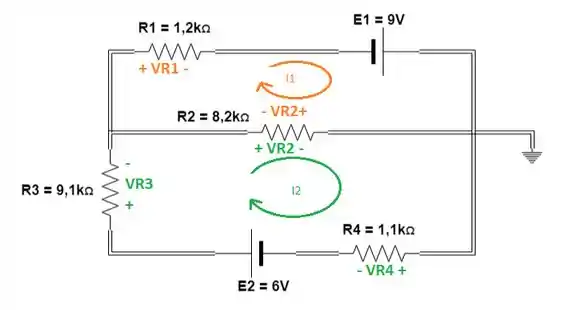
Passo 3
Pela LKT, podemos escrever a malha 1 como:
Pela LKT, podemos escrever a malha 2 como:
Passo 4
Pela equação 1, podemos definir que:
Substituindo na segunda equação:
Achamos que . Assim, .
Passo 5
Percebemos que a corrente que passa pelo resistor é a diferença entre as correntes e . Assim o sentido será definido pela maior corrente, nesse caso o sentido é o da corrente e o seu valor é:
Resposta
Exercícios de Livros Relacionados
Usando a análise de malhas. calcule v1.
Selecione a árvore do resistor de 4 Ω e do resistor de 2 Ω com a tensão v 1 e use o método de conjunto de corte para calcular v .
Resolva o Problema 4.13 usando o método das correntes de malha.
a) Use o método das correntes de malha para determinar quais fontes no circuito da Figura P4.48 estão fornecendo potência.b) Determine a potência total dissipada no circuito.
Resolva o Problema 4.27 usando o método das correntes de malha.