Use a análise de malhas para determinar , e no circuito da figura abaixo:
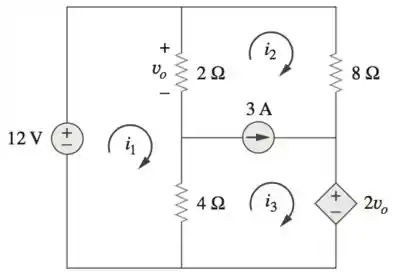
Passo 1
Vamos lá! A malha 2 e a malha 3, onde se encontram as correntes e , é considerada uma SUPERMALHA.
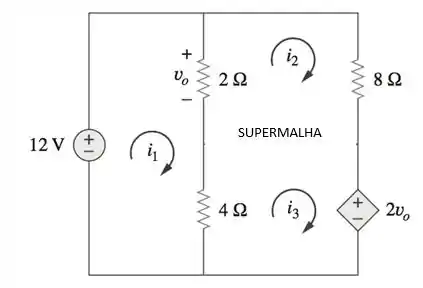
Portanto as equações segundo LTK são:
Passo 2
Aplicando a lei de Ohm no resistor de :
Substituindo no sistema e simplificando:
Passo 3
Até o momento, temos duas equações e três incógnitas. Precisamos encontrar mais uma equação que relacione as correntes de malha. Para isso, vamos escolher o nó onde aplicaremos a LCK:
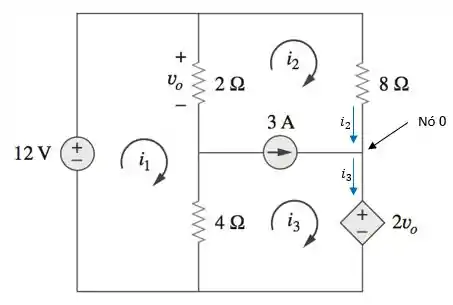
Aplicando a LCK no nó :
Pronto, agora temos três equações e três incógnitas:
Passo 4
Agora, vamos resolver esse sistema aí de cima! Isolando na terceira equação:
Substituindo a relação acima na primeira e na segunda equação:
Simplificando:
Somando as duas equações:
Logo:
Finalmente:
Resposta
Exercícios de Livros Relacionados
Usando a análise de malhas. calcule v1.
Selecione a árvore do resistor de 4 Ω e do resistor de 2 Ω com a tensão v 1 e use o método de conjunto de corte para calcular v .
Resolva o Problema 4.13 usando o método das correntes de malha.
a) Use o método das correntes de malha para determinar quais fontes no circuito da Figura P4.48 estão fornecendo potência.b) Determine a potência total dissipada no circuito.
Resolva o Problema 4.27 usando o método das correntes de malha.