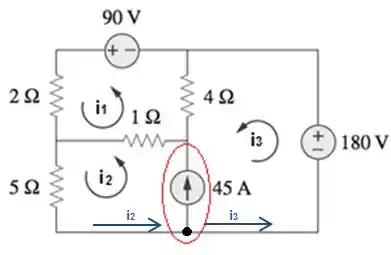
Use análise de malhas para determinar no circuito da figura abaixo
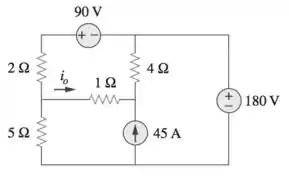
Considerando a malha que contém a fonte de como a malha 1, a malha abaixo como a malha 2 e a malha da fonte de como a malha 3. As correntes , e , são pertencentes respectivamente as malhas 1, 2 e 3.
Passo 1
Identificando as malhas:
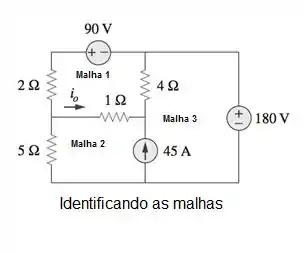
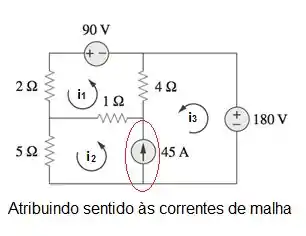
Atribuir sentido às correntes de malha:
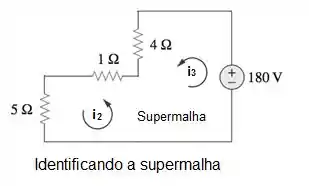
Se você analisar o circuito, vai perceber que entre as malhas 2 e 3 existe uma supermalha:
Passo 2
Depois de analisar o circuito, vamos equacioná-lo, utilizando a LTK e levando em consideração a supermalha:
Simplificando:
Se você perceber, há duas equações e 3 incógnitas. Por isso precisamos aplicar a LCK no nó da supermalha. Fica tranquilo, vamos ver isso no passo seguinte :)
Passo 3
Passo 4
Analisando o nó da supermalha e aplicando LCK:
Com esta equação, podemos resolver o sistema agora:
Passo 5
Substituindo a equação em e :
Resolvendo o sistema:
Somando as duas equações, fica somente:
Passo 6
Se analisarmos o circuito novamente, veremos que:
Substituindo o valor de na equação :
De acordo com a equação :
Passo 7
Finalmente,