Exercícios Resolvidos de Ângulo de Torção e Problemas Estaticamente Indeterminados
Ver TeoriaEnunciado
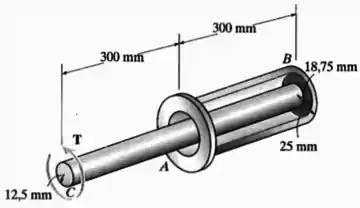
O dispositivo serve como uma mola de torção compacta. É feito de aço A-36 e composto por um eixo interno maciço embutido em um tubo e acoplado a esse tubo por um anel rígido em . Podemos considerar que o anel em também é rígido e está preso de modo que não pode girar. Se a tensão de cisalhamento admissível para o material for e o ângulo de torção em estiver limitado a , determine o torque máximo que pode ser aplicado na extremidade .
Dados: .
Passo 1
O que está acontecendo?
O eixo maciço possui um raio enquanto que o tubo possui um raio externo e um raio interno .
O eixo tem um comprimento enquanto que o tubo tem um comprimento .
Ambos possuem um módulo de elasticidade transversal .
E ambos estão submetidos ao mesmo torque , sendo que, a partir desse torque, é possível calcular:
1. Tanto a tensão de cisalhamento máxima em cada peça, usando a fórmula da torção:
2. Quanto o ângulo de torção em cada peça, usando a sua fórmula:
E o que é que o exercício quer?
Ele quer que a gente determine o torque máximo que pode ser aplicado nessa dispositivo, tendo em mente que:
1. A tensão de cisalhamento máxima tanto no tubo quando no eixo não pode ultrapassar a tensão de cisalhamento admissível :
& 2. O ângulo de torção em (), que é igual à soma dos ângulos de torção do tubo () e do eixo (), não pode ultrapassar o limite :
Passo 2
Vamos começar o exercício verificando as condições relativas à tensão de cisalhamento máxima:
Aplicando a fórmula da torção para o tubo e para o eixo (ambos submetidos ao mesmo torque ), essas condições acima ficam assim:
Como o tubo possui um raio externo e um raio interno , o seu momento de inércia polar vai ser:
Já para o eixo , maciço, vamos ter que:
Substituindo essas fórmulas nas expressões anteriores, vamos ter que:
Queremos avaliar qual é o torque máximo que pode ser aplicado, então devemos isolá-lo.
Fazendo isso, as nossas expressões ficam assim:
Ainda podemos arrumar essas expressões, deixando elas assim:
Agora, substituímos os valores:
- ;
- ;
- ;
- & ,
Para encontrarmos que:
Como esses números são muito grandes, podemos reescrevê-los em , encontrando assim as seguintes condições limitantes do torque :
Passo 3
Agora, vamos verificar a condição referente aos ângulos de torção:
Aplicando a fórmula do ângulo de torção para o tubo e para o eixo (ambos submetidos ao mesmo torque ), essa condição acima fica assim:
Colocando em evidência, temos que:
E isolando o torque , encontramos que:
Substituindo as fórmulas dos momentos polares de inércia , já definidas no passo anterior, isso tudo fica assim:
Sim, isso está meio assustador...
Mas não é nada que uma arrumadinha não resolva.
Dá para colocar o em evidência, por exemplo:
E aí multiplicar essa expressão por esse termo invertido, ou seja, por :
E pronto, já ficou um pouco melhor a cara da expressão!
Agora, a tentação é substituir os valores:
- ;
- ;
- ;
- ;
- ;
- ;
- & ,
E encontrar o valor máximo para o torque .
Mas a verdade é que ainda não podemos fazer isso.
Isso porque não podemos usar o valor .
Se usarmos ele, o nosso resultado final para vai sair em uma unidade bizarra como (graus).
Precisamos converter esse valor de para radianos!
Para fazer isso, multiplicamos ele por :
E encontramos que:
Agora sim, podemos substituir e calcular tudo.
Fazendo isso, vamos encontrar que:
Para deixar esse resultado em uma unidade mais usual, reescrevemos ele em , encontrando assim a nossa terceira e última condição limitante para o torque :
Passo 4
Comparando as três condições encontradas, vemos que a condição mais limitante é a condição :
Dessa forma, temos que o maior torque que pode ser aplicado no ponto do dispositivo desse exercício é: