Exercícios Resolvidos de Ângulo de Torção e Problemas Estaticamente Indeterminados
Ver TeoriaEnunciado
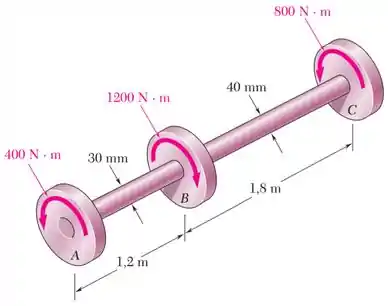
Os torques mostrados são aplicados nas polias , e . Sabendo que ambos os eixos têm seção transversal cheia e são feitos de latão (), determine o ângulo de torção entre e e e .
Passo 1
O que está acontecendo?
O eixo é composto pelos segmentos:
- , de comprimento , diâmetro , e, consequentemente, raio ;
- & , de comprimento , diâmetro , e, consequentemente, raio .
Ambos os segmentos são feitos de latão, com um módulo de elasticidade transversal .
Além disso, eixo é carregado com torques externos nos seus pontos , e , como mostra o seu DCL (diagrama de corpo livre) abaixo, feito utilizando a regra da mão direita:
A partir desse DCL, é possível fazer uma análise dos esforços internos para descobrir o valor dos torques internos e nos segmentos e do eixo, respectivamente.
E o que é que o exercício quer?
Ele quer que a gente determine o ângulo de torção entre os pontos e () e entre os pontos e ().
Para calcular , que é o ângulo de torção do segmento do eixo, podemos usar a fórmula do ângulo de torção:
Além disso, também podemos usar essa fórmula para calcular o ângulo de torção do segmento do eixo, .
Daí que, somando com , vamos encontrar :
Passo 2
Vamos começar o exercício fazendo uma análise dos esforços internos na peça para identificar os valores dos torques internos nos trechos e , e .
Primeiro, fazemos seções dentro desses trechos e desenhamos os torques internos desconhecidos:
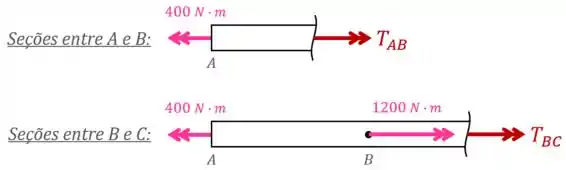
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Em seguida, aplicamos o equilíbrio de torques para cada trecho:
Isolando os torques desconhecidos e nessas equações, encontramos que:
Passo 3
Agora, podemos calcular os ângulos de torção dos segmentos e usando a fórmula:
Primeiro, temos que ambos esses segmentos possuem seções circulares maciças, e assim, tem um momento de inércia polar .
Usando isso, temos que:
Arrumando tudo, isso fica assim:
Agora, aplicando essa expressão para o segmento , temos:
Substituindo:
- ;
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
Encontramos que:
O que nos dá a resposta do item :
Já aplicando a expressão para o segmento , temos:
Substituindo:
Encontramos que:
Passo 4
Encontrados e , podemos soma-los para encontrar :
Substituindo os valores encontrados, temos que:
Calculando isso, encontramos a nossa resposta para o item :
Passo 5
Apesar de que o exercício não especificou no enunciado que ele queria os resultados em graus () e não em radianos (), ele forneceu o gabarito final em graus.
A verdade é que muitos professores preferem resultados em graus, então precisamos saber fazer essa conversão.
Lembra aí...
Você pode converter radianos para graus usando a relação de que equivale à :
Ou seja:
Substituindo isso nas nossas respostas, vamos ter que:
Calculando tudo, encontramos as nossas respostas finais: