Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Ângulo de Torção e Problemas Estaticamente Indeterminados

Ver Teoria
Exercício 21345678910

Enunciado

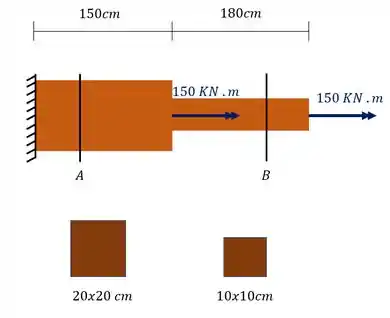
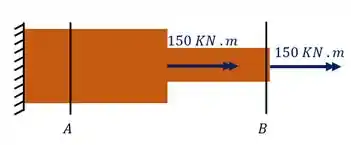
Na figura abaixo temos uma barra de madeira com seção retangular que varia conforme mostrado na figura. Usando seus conhecimentos relacionados a ângulo de torção, determine as deformações angulares em graus das seções A e B marcadas na figura.

u s e   G = 27 G P a

Passo 1

Como ele quer que determinemos o nosso ângulo de torção, precisaremos usar a nossa fórmula de deformação angular que é dada por

ϕ = T   . L G   .   J

Olhando a nossa fórmula temos dois valores que determinamos facilmente

Um é o comprimento e o outro é o módulo de elasticidade transversal, chamando a barra mais fina de B e a mais grossa de A, teremos que

L A = 150 c m

L B = 180 c m  

O modulo de elasticidade transversal é o mesmo para ambas, já que se trata do mesmo material, logo

G = 27   G P a

Passo 2

Outra coisa que precisamos determinar é o momento polar de inercia, para isso temos que lembrar do seguinte conceito.

J = I y y + I z z

Vale ressaltar que essa relação só vale para os casos em que não ocorrer empenamento da nossa peça, se por acaso você fizer um exercício em que há empenamento da peça, essa relação não poderá ser usada.

Como para seções retangulares nos temos que

I z z = B H 3 12

I y y = H B 3 12

Teremos que o momento polar de inercia será

J = I y y + I z z

J = H B 3 12 + B H 3 12

J = B H H 2 + B 2 12

Como se trata de uma seção quadrada teremos que B = H . Substituindo teremos que

J = H . H H 2 + H 2 12 = 2 H 4 12 = H 4 6

Logo para menor seção teremos que

J B = 0,1 4 6 = 1,67   .   10 - 5 m 4

E para seção maior teremos que

J A = 0,2 4 6 = 2,67   .   10 - 4 m 4

Passo 3

Por fim basta apenas determinar o valor do momento torsor em cada uma das seções, dividindo a nossa barra na seção A teremos que

Para sabermos o torque que age nessa seção devemos levar até ela todos os esforços que sumiram após fazermos o corte, logo teremos que os esforços que agem nessa seção são

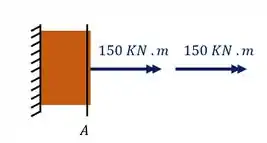
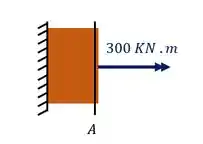
Logo na nossa seção A o toque atuante é

T A = 300   K N . m

Agora dividindo a nossa barra na seção B teremos que

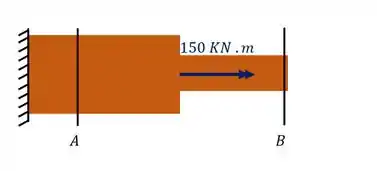
Para sabermos o torque que age nessa seção devemos levar até ela todos os esforços que sumiram após fazermos o corte, logo teremos que o esforço que age nessa seção é

Logo na nossa seção B o toque atuante é

T B = 150   K N . m

Passo 4

Como já temos os valores que precisávamos, basta substituirmos na nossa equação.

Temos que

L A = 150 c m = 1,5   m

G = 27   G P a = 27000000 K N m 2

J A = 2,67   .   10 - 4 m 4

T A = 300   K N . m

Logo para nossa seção A teremos que

ϕ A = T A   . L A G   .   J A

ϕ A = 300   .   1,5 27000000   . 2,67   .   10 - 4 = 0,062   R a d

Também temos que

L B = 180 c m = 1,8   m

G = 27   G P a = 27000000 K N m 2

J B = 1,67   .   10 - 5 m 4

T B = 150   K N . m

Mas calma, ao usar a fórmulinha, achamos o ângulo de B em relação a A . Logo para nossa seção B teremos que

ϕ B \ A = T B   . L B G   .   J B

ϕ B \ A = 150   .   1,8 27000000   . 1,67   .   10 - 5 = 0,6   R a d

Como queremos as nossas deformações angulares em graus teremos que fazer regra de 3

π - - - - - - 180 °

ϕ - - - - - - - x °

Fazendo isso teremos que

ϕ A = 0,062   R a d = 3,55 °

ϕ B \ A = 0,6   R a d = 34,38 °

Aí para achar o ângulo de torção de B em relação ao apoio (começo da barra), a gente o soma com o ângulo de A :

ϕ B = ϕ B \ A + ϕ A = 37,93 °

Resposta

ϕ A = 0,062   R a d = 3,55 °

ϕ B = 0,6 62   R a d = 37,93 °

Exercícios de Livros Relacionados

A seção transversal cheia mostrada é feita de aço elastoplástico com T E = 145M P aeG = 77,2G P a . O torque é aumentado em intensidade até que o eixo tenha sido girado em 6°; em seguida, o torque é r
Um tacômetro F, utilizado para registrar em forma digital a rotação do eixo A, é conectado ao eixo por meio do trem de engrenagens mostrado, valendo-se de quatro engrenagens e três eixos de aço de seç
Uma placa anelar de espessura t e módulo de elasticidade transversal G é usada para conectar o Eixo AB de raio r 1 ao tubo CD de raio interno r 2 . Sabendo-se que o torque T é aplicado à extremidade A
Dois eixos de aço sólidos são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimencionados de modo que permitam uma rotação relativa
O eixo é composto por uma seção maciça de aço A B e uma porção tubular feita de aço com núcleo de latão. Se o eixo estiver preso a um apoio rígido A e for aplicado um torque T =50N ⋅ m a ele em C , de