Exercícios Resolvidos de Ângulo de Torção e Problemas Estaticamente Indeterminados
Ver TeoriaEnunciado
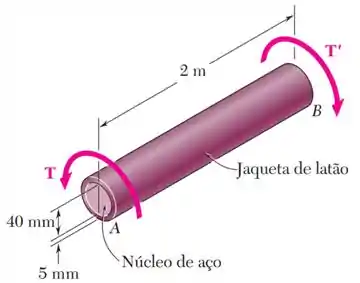
O eixo composto mostrado consiste em uma jaqueta de latão de de espessura () unido a um núcleo de aço de de diâmetro (). Sabendo que o eixo está submetido a um torque de , determine a tensão de cisalhamento máxima na jaqueta de latão, a tensão de cisalhamento máxima no núcleo de aço e o ângulo de torção de relativo a .
Passo 1
O que está acontecendo?
A jaqueta de latão tem:
- Um diâmetro interno de , e, consequentemente, um raio interno ;
- Uma espessura , e, consequentemente, um raio externo ;
- E um módulo de elasticidade transversal .
Já o núcleo de aço tem:
- Um diâmetro de , e, consequentemente, um raio ;
- E um módulo de elasticidade transversal .
Ambas as peças possuem um comprimento e estão suportando, juntas, a um torque de .
Como as peças estão suportando esse torque juntas, temos que a soma dos torques suportados pela jaqueta de latão e pelo núcleo de aço deve ser igual ao torque total:
Mas essa relação não é suficiente para que a gente possa determinar os valores dos torques e suportados por cada peça.
Então vamos ter que recorrer a uma equação de compatibilidade.
Qual vai ser a equação de compatibilidade nesse caso?
Nesse caso, temos que a jaqueta de latão e o núcleo de aço se torcem juntos.
Dessa forma, eles vão possuir o mesmo ângulo de torção :
Essa vai ser a nossa equação de compatibilidade.
Para que ela seja útil, vamos ter que aplicar, para cada peça, a fórmula do ângulo de torção:
Assim, vamos poder usar a equação de compatibilidade para relacionar os torques e .
E o que é que o exercício quer?
Nos itens e , ele quer saber as tensões de cisalhamento máximas na jaqueta de latão e no núcleo de aço, respectivamente.
Para calcular essas tensões, vamos primeiro encontrar os torques e suportados por cada peça, para, em seguida, aplicar a fórmula da torção:
Já no item , ele quer saber o ângulo de torção do conjunto, que vai ser igual tanto ao ângulo de torção do latão quando ao ângulo de torção do aço:
Assim, podemos escolher entre calcular ou para determinar o ângulo de torção do conjunto.
Passo 2
Então como vimos, do equilíbrio de torques, temos que:
Mas essa relação não é suficiente para calcular os torques desconhecidos e .
Então...
Vamos recorrer à equação de compatibilidade:
Aplicando a fórmula do ângulo de torção para o latão e para o aço (e tendo em mente que ambas as peças tem o mesmo comprimento ), isso fica assim:
Cortando com , temos que:
E isolando , encontramos que:
Agora, da Equação 1, temos que .
Sendo assim, temos que:
Em seguida, passando para o outro lado:
E colocando em evidência:
Encontramos que:
Agora, podemos identificar que:
- A jaqueta de latão vai ter um momento de inércia polar ;
- Enquanto que, para o núcleo de aço, que é maciço, .
Dessa forma, temos que:
Cortando com , isso significa que:
Finalmente, substituindo os valores:
- ;
- e ;
- & , e ,
Vamos encontrar que:
E como da Equação 1, temos que:
Podemos substituir e para encontrarmos que:
Passo 3
Agora que já conhecemos os torques e em cada peça, já podemos calcular as tensões de cisalhamento máxima em cada uma delas.
Para tanto, usamos a fórmula da torção:
Aplicando essa fórmula para a jaqueta de latão, vamos ter que:
Substituindo , isso fica assim:
Arrumando tudo, temos que:
Por fim, substituindo:
- ;
- & ,
- ;
- & ,
Encontramos que:
E como , isso significa que:
O que é a nossa resposta para o item !
Agora, aplicando a mesma fórmula, mas para o núcleo de aço, temos que:
Substituindo , isso fica assim:
E simplificando tudo, temos que:
Finalmente, substituindo:
Encontramos nossa resposta para o item :
Passo 4
Agora só falta o item : calcular o ângulo de torção.
Para tanto, vamos optar por calcular o ângulo de torção no núcleo de aço:
Aplicando a fórmula do ângulo de torção para o núcleo de aço, que possui um comprimento , temos que:
Como o núcleo de aço tem seção transversal circular e maciça de raio , temos que , de tal forma que:
Agora, substituindo os valores:
- ;
- ;
- ;
- & ,
Vamos encontrar que:
Multiplicando esse resultado por , conseguimos convertê-lo para graus:
Calculando tudo, encontramos nossa resposta para o item e finalizamos o exercício: