Exercícios Resolvidos de Ângulo de Torção e Problemas Estaticamente Indeterminados
Ver TeoriaEnunciado
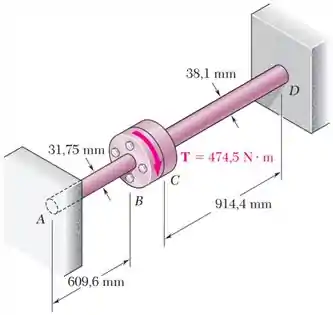
Dois eixos sólidos de aço são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimensionados de modo que permitam uma rotação relativa entre as flanges de até antes que ambas passem a girar juntas.
Sabendo que , determine a máxima tensão de cisalhamento em cada eixo quando um torque de intensidade igual a é aplicado na flange .
Passo 1
O que está acontecendo?
Os eixos maciços e tem diâmetros e , e, consequentemente, raios e .
Além disso, eles têm comprimentos e e o mesmo módulo de elasticidade transversal .
Um torque é aplicado em e, para manter o equilíbrio das peças, as paredes aplicam torques de reação e em e .
Usando a regra da mão direita, podemos fazer um DCL (diagrama de corpo livre) para visualizar todos esses torques:
Agora...
Fazendo o equilíbrio de torques no DCL acima, vamos encontrar que:
Mas essa relação não é suficiente para que a gente saiba o valor dos torques e , então vamos ter que recorrer a uma equação de compatibilidade.
E qual vai ser a equação de compatibilidade nesse caso?
Então...
Lá em “Carga Axial”, talvez você tenha resolvido alguns exercícios em que haviam folgas entre as peças.
Lá, quando a gente tinha duas peças entre duas paredes e uma folga entre as peças, tínhamos que:
Ou seja, a nossa equação de compatibilidade era:
Agora, temos mais uma vez duas peças entre duas paredes e uma folga entre essas peças.
Mas dessa vez, temos um problema de torção.
Então ao invés de variações de comprimento , vamos ter ângulos de torção :
Como no nosso caso a peça 1 é o eixo , a peça 2 é o eixo e a folga é de , a nossa equação de compatibilidade vai ser:
Sendo que os ângulos de torção podem ser descritos pela sua fórmula:
E o que é que o exercício quer!?!??
Ele quer que a gente calcular as tensões de cisalhamento máximas em cada eixo, que vão ser dadas pela fórmula da torção:
Agora, para calcular essas tensões em cada eixo, vamos ter que:
1. Identificar quais são os torques internos nos eixos e ;
& 2. Usar a equação de compatibilidade para calcular esses torques internos .
Passo 2
Então vamos começar identificando os torques internos em cada eixo.
Começamos pelo DCL do conjunto:
E em seguida fazemos uma análise dos esforços internos: secionamos o conjunto em seus diferentes trechos e observamos os esforços internos nas seções.
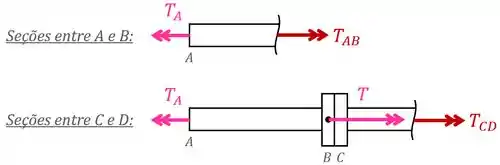
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Aplicando o equilíbrio de torques para cada caso, temos que:
E isolando os torques internos e , encontramos que:
Passo 3
Agora que já identificamos os torques internos, já podemos desenvolver a nossa equação de compatibilidade:
Aqui, vamos aplicar a fórmula do ângulo de torção para calcular os ângulos e .
Mas a fórmula do ângulo de torção fornece resultados em radianos ().
Então antes de tudo, vamos converter a folga de para radianos.
Para tanto, multiplicamos ela por :
Calculando tudo, encontramos que:
Agora sim, podemos aplicar a fórmula do ângulo de torção para os eixos e , ambos de mesmo módulo de elasticidade transversal :
Como os eixos e são maciços, podemos substituir para eles.
Além disso, podemos substituir que e que .
Fazendo tudo isso, temos que:
Em seguida, podemos tirar em evidência:
E passar esse termo para o outro lado:
Podemos arrumar a equação para deixa-la assim:
E colocar em evidência:
E, finalmente, podemos isolar , para encontrar que:
Agora, substituímos os valores:
- ;
- ;
- e ;
- & e ,
Para encontrarmos o valor de :
Sendo que esse valor poder ser reescrito em :
Passo 4
Conhecendo , podemos agora fazer o cálculo dos valores dos torques internos e nos eixos.
Primeiro, temos que:
Como , isso significa que:
Em seguida, temos que:
Como e , isso significa que:
O que dá:
Passo 5
Calculados os torques internos, podemos calcular as tensões de cisalhamento máximas em cada eixo.
Para tanto, vamos usar a fórmula da torção:
Como os dois eixos são maciços, temos que para ambos.
Dessa forma, temos que:
Arrumando tudo, isso fica assim:
Aplicando essa fórmula para os eixos e , vamos ter:
Em seguida, substituindo os valores:
- ;
- ;
- ;
- & ,
Encontramos que:
Por fim, antes de escrevermos a nossa resposta final, podemos perceber duas coisas.
Primeiro, que ao querer saber qual é a tensão de cisalhamento máxima em cada eixo, o exercício só quer saber a intensidade de .
Então podemos retirar o sinal de negativo de .
E segundo, que é o mesmo que .
Tendo tudo isso em mente, definimos a nossa resposta final: