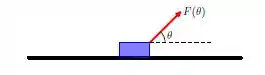
A intensidade da força necessária para arrastar uma caixa de M Kg sobre uma superfície horizontal puxando-a com uma corda com ângulo é dada por:
onde e é uma constante denominada coeficiente de fricção. Use aproximação linear de primeira ordem para estimar a força necessária para arrastar uma caixa de 40 kg, sabendo que e que a corda faz um ângulo de 46° em relação à superfície.
Passo 1
Primeiro de tudo a gente precisa lembrar da equação de aproximação linear:
Onde temos que
Ou seja, temos que com os valores dados no enunciado. E depois a gente vai precisar derivar essa função também e utilizar os valores dados no enunciado.
Vamos precisar usar a regra da cadeia...vem comigo pro passo 2!!
Passo 2
Fazendo a regra da cadeia:
Substituindo e simplificando, temos:
Ou seja, nossa é igual a:
Substituindo os valores, temos:
Logo, tem-se: