Suponha que , , sejam variáveis aleatórias independentes, cada uma delas tendo distribuição de Poisson com parâmetro . Faça . Observação: a soma de variáveis aleatórias de Poisson independentes tem distribuição de Poisson.
(a) Empregando o Teorema Central do Limite, calcule uma aproximação para .
OBS: Aqui se trata de aproximar uma distribuição discreta por uma contínua. Então, da mesma forma como foi visto no caso da aproximação de Binomial por Normal, cabe usar uma correção de continuidade.
Passo 1
Temos que:
E como vimos lá na teoria, a esperança e a variância de uma v.a. que segue uma Poisson são o próprio parâmetro . Então:
E o enunciado também falou pra gente de uma outra v.a., , que é a soma de todos os :
E ele fala pra gente que no enunciado que a soma de variáveis de Poisson é uma variável de Poisson, então:
E o parâmetro dela vai ser vezes o , já que temos variáveis de Poisson com parâmetro aí dentro!
Então, verdadeiramente, o vai seguir uma Poisson, mas repara comigo: como temos muiiiitos (, é muito!), e eles seguem a mesma distribuição e são independentes, tudo indica que é um bom caso pra aproximarmos a soma dos (ou seja, nossa v.a. ) pela distribuição Normal.
Pra não confundir, vamos chamar aproximação de por . Isso dá pra gente:
Passo 2
Letra a)
Pra gente calcular uma aproximação de , vamos usar nossa aproximação de pela Normal, ou seja, . Porééém, é uma v.a. discreta, lembra? Ela verdadeiramente segue uma Poisson! E é uma v.a. contínua!
Então vamos ter que corrigir o erro de continuidade entre elas antes de calcular essa probabilidade. Assim ó:
Por que virou 2,5 mesmo? Dá uma olhada no gráfico:
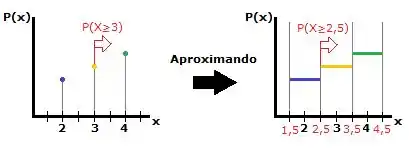
Ou então se você não estiver afim de desenhar gráfico pra pensar, lembra da fórmula:
Beleza, corrigimos o erro de continuidade, então podemos partir pro cálculo da probabilidade. Como? Calculando probabilidade de Normal como a gente sempre faz, PADRONIZANDO! Bora lá:
Agora pega aí sua tabela da Normal e vê quem é a probabilidade no corpo da tabela correspondente para esse :
E isso dá pra gente:
E essa aí é nossa probabilidade aproximada! =)
Resposta
Letra a)