Uma coluna de aço tem comprimento de e está apoiada por pinos em ambas as extremidades. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica.
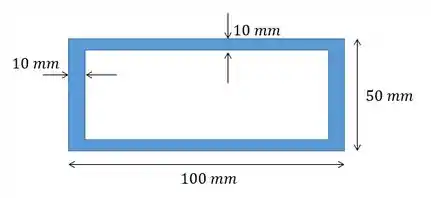
Passo 1
Bom, pessoal, vamos lá resolver mais um exercício! Esse aqui não tem muitos segredos é só lembrar que a equação da flambagem para extremidades apoiadas em pinos é:
Aí temos de lembrar também que o coeficiente de elasticidade do aço é . Além disso o problema forneceu os dados: e nos deu a seção transversal para calcularmos .
Então basta calcular e substituir na equação, aí acabou!
Passo 2
Vamos calcular o momento de inércia. Percebam que temos dois eixos:
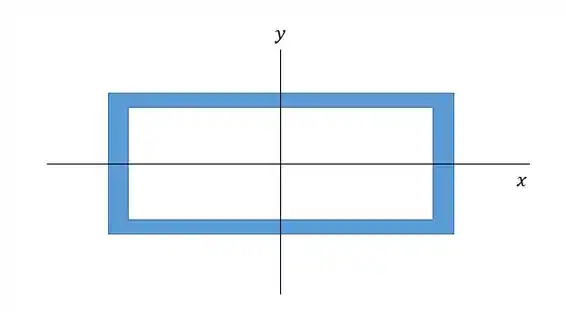
Como trata-se de um retângulo nós vamos ter que o momento de inércia emc ada eixo é diferente, aí a gente tem que lembrar que a flambagem ocorre no eixo de menor momento de inércia.
A equação do momento de inércia para uma barra retangular é:
Se nos queremos o menor momento de inércia então devemos escolher o menor lado para ser a altura (já que a altura que está sendo elevada ao cubo). Isso faz sentido não faz? Logo, vamos ter que a base vai ser o nosso eixo mesmo e a altura no eixo .
Mas a nossa seção é vazada então devemos subtrair o termo de dentro:
Passo 3
Agora é só substituir na equação da flabagem:
Passo 4
Pra finalizar vamos ver se a nossa barra resiste ao escoamento por compressão:
Calculando a área nós temos:
Como a tensão de escoamento do aço é então a carga de pode ser aplicada à coluna sem risco de escoar.