Uma engenheira deve projetar uma coluna para suportar uma carga total . Sabendo que o projeto admite apenas dois tipos de colunas do mesmo material, área e comprimento mas uma retangular e outra circular. Qual coluna a projetista deve utilizar se estiver interessado exclusivamente na maior estabilidade possível?

Para responder essa questão da maneira mais correta possível a gente tem que lembrar da equação da flambagem com relação à carga crítica:

O problema nos fala que as colunas tem o mesmo comprimento e são feitas do mesmo material logo e são irrelevantes na análise deste problema, também é.

Logo a carga crítica vai ser proporcional ao momento de inércia da coluna

Ou seja, devemos escolher aquela que nos fornece o maior momento de inércia porque assim a coluna consegue suportar uma carga crítica maior.

Vamos olhar novamente as nossas colunas, agora com dois eixos apontados:

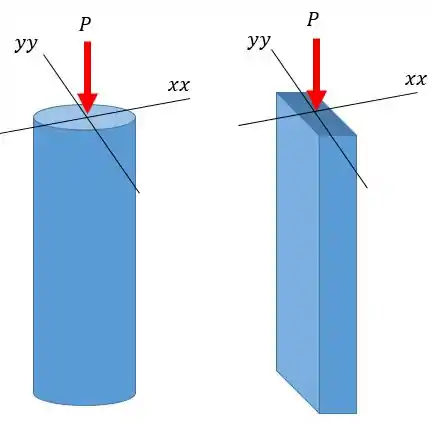
Não acho que seja necessário ficar calculando o momento de inércia de cada eixo, mas para refrescar sua memória o momento de inércia é calculado como:

Pessoal, pouco me interessam esses valores, sabe por quê? Como ambas tem a mesma área então o momento de inércia de um dos eixos da coluna retangular vai ser maior do que o do círculo e o outro menor. Podemos escrever como:

Correto? O momento de inércia do círculo é igual em qualquer direção, só pra lembrar.

Agora a gente só precisa lembrar que a flambagem é uma danada e sempre vai ocorrer em torno do menor momento de inércia.

Sendo assim, não interessa que a coluna retangular tem um eixo com o momento de inércia maior, porque vamos analisar sempre o menor momento de inércia.

Logo, a coluna circular é mais estável que a retangular =D

Colunas quadradas também são boas já que possuem o mesmo momento de inércia em ambas as direções. No quesito estabilidade, quanto mais homogênea for a distribuição dos momentos de inércia melhor!

A coluna circular é mais estável que a retangular.