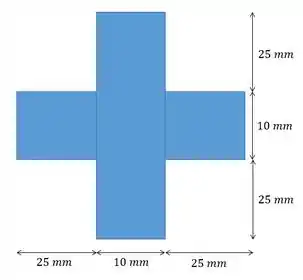
Uma coluna de aço tem comprimento de e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica.
Passo 1
E aííí, meus queridos e minhas queridas, tudo belezinha? Vamos resolver essa questãozinha aí que nos pede a carga crítica. Pra começar é importante frisar que o problema nos diz que a coluna está apoiada em pinos, logo a equação da carga crítica é:
O problema nos disse que é um aço , que tem , e também forneceu o comprimento da coluna de . Então para achar a carga crítica basta a gente calcular o momento de inércia e substituir na equação!
Passo 2
Antes de sair calculando o momento de inércia igual a uns loucos vamos pensar um pouco...

Uma seção transversal, assim como a fornecida pelo problema, tem diferentes momentos de inércia dependendo do eixo a qual estamos analisando. A flambagem sempre vai acontecer no eixo mais fraco, beleza?
Mas você, que é muito inteligente que eu sei, já percebeu que a figura é simétrica então o momento de inércia em é igual ao momento de inércia em . Ahhh, então suave, nesse caso não precisamos nos preocupar muito com a direção, portanto:
Agora para calcular a gente tem uma figura composta por duas barras, então vamos calcular cada barra separadamente e somar os momentos resultantes:
Aí aqui não tem muito segredo, a base de uma é igual a altura da outra, logo:
E
Passo 3
Agora é só substituir na equação da força crítica:
Passo 4
Pessoal, a gente já até achou a carga crítica mas é importante também saber se não ultrapassamos o limite de escoamento do material também. Como o aço tem , então a gente vai fazer:
A área da seção eu vou calcular como um quadradão () menos 4 quadradinhos :
Então vamos ter:
Como essa tensão é menor do que então a nossa coluna pode ser utilizada no projeto já que não irá flambar e nem escoar =D