Uma força de é aplicada ao sistema mecânica mostrado. Sabendo que todas as hastes são de aço . Determine se a coluna vertical sofrerá flambagem. Dado: As hastes possuem índice de esbeltez igual a e área igual a .
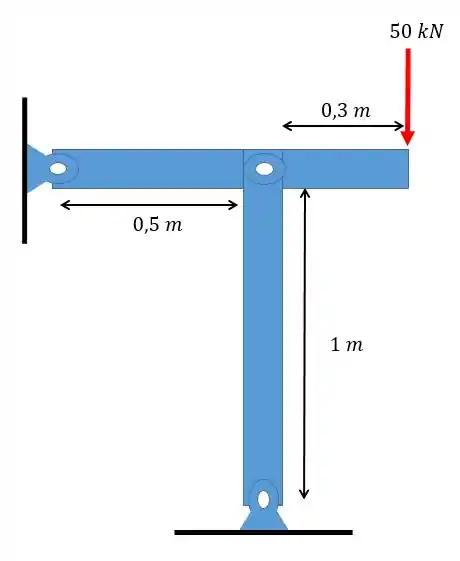
Passo 1
Pessoal, esse problema pede para calcularmos a tensão crítica de flambagem e nos deu o índice de esbeltez, vamos lembrar o que isso significa!
Índice de esbeltez é a relação entre o comprimento e o raio de giração da coluna
Isso é importante porque podemos calcular a tensão crítica a partir dessa grandeza, já que a tensão crítica pode ser calculada como:
Dessa forma, para resolver essa questão basta acharmos a tensão crítica a partir da equação da flambagem a cima e comparar com a tensão de compressão da nossa coluna.
Passo 2
Vamos calcular a tensão de compressão da coluna, para isso vamos fazer um diagrama de forças:
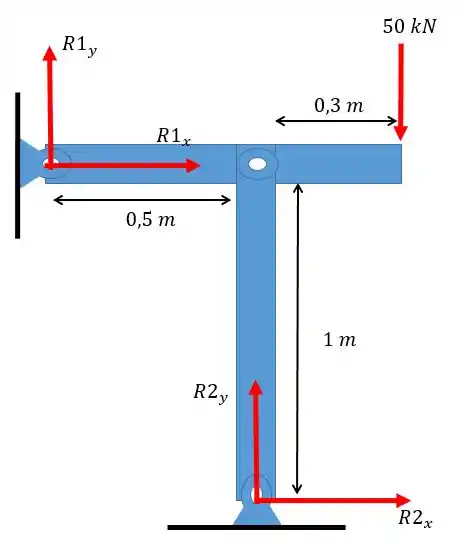
Agora percebam que as componentes horizontais não são importantes para o cálculo da flambagem da coluna vertical, por isso iremos queremos apenas dessa maneira podemos fazer aplicar o somatório dos momentos em torno da junção das hastes:
Pessoal, aqui é importante perceber que estamos olhando só para a barra horizontal, logo a força não entra nas nossas continhas.
Agora é só aplicar o somatório das forças em :
Passo 3
Para achar a tensão de compressão é só dividir pela área:
Vamos converter a área para metros:
Beleza, já temos a pressão a qual a nossa haste está submetida. Vamos achar agora a tensão crítica de flambagem
Passo 4
Agora é só substituir na equação da flambagem e achar a carga crítica:
Passo 5
Como a tensão de compressão é bem menor do que a tensão crítica de flambagem a nossa haste não sofrerá com a flambagem.
Passo 6
Como a tensão de compressão é bem menor do que a tensão crítica de flambagem a nossa haste não sofrerá com a flambagem.
Resposta
Ei, a resposta está no passo a passo :)