Num projeto mecânico uma carga deve ser elevada por um pistão de aço no formato tubular com diâmetro externo de e espessura de . Sabendo que podemos considerar as extremidades desse pistão apoiadas por pinos calcule a máxima carga que esse pistão pode suportar sem sofrer flambagem. Dados: , comprimento do pistão .
Passo 1
Olá, pessoas!! Vamos resolver mais uma questãozinha de flambagem. Essa questão é bem direta e nos pede a máxima carga que o pistão pode suportar, aqui o pistão vai agir como se fosse uma coluna e queremos achar o .
Dessa forma vamos utilizar a equação:
Aí só precisamos calcular o momento de inércia e substituir na equação =)
Passo 2
Vamos calcular o momento de inércia então. Lembrando que para um círculo vamos ter:
Mas o pistão é um tubo vazado, então vamos ter o seguinte:
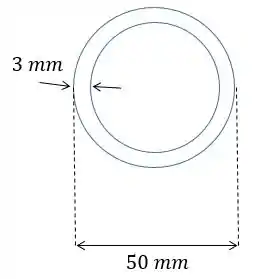
Assim,
Para achar o momento de inércia vamos fazer:
Substituindo os valores em metros vamos ter:
Passo 3
Agora é só substituir na equação
Passo 4
Resposta
Ei, a resposta está no passo a passo :)