Uma estrutura mecânica está apoiada com liberdade de giro sobre colunas de aço () com comprimento de . Sabendo que nessa coluna é utilizado o perfil de abas largas , qual o valor máximo da carga que pode ser aplicada sobre a coluna de modo a não haver falha nem por escoamento nem por instabilidade. Considere .
Passo 1
Meus amigos e minhas amigas, essa questão está falando sobre falha por escoamento e por instabilidade (flambagem). Logo vamos ter que fazer as duas análises para ter certeza que não vai dar ruim na nossa coluna.

Então vamos fazer primeiramente a análise de estabilidade e achar a carga crítica por meio da nossa equação da flambagem para colunas apoiadas em pinos (por causa da liberdade de giro):
depois vamos utilizar essa carga crítica para ver se não vai ocorrer escoamento:
Passo 2
Como o problema nos forneceu o perfil da barra a gente não precisa calcular o momento de inércia é só ir numa tabela de perfis de abas largas e achar . Aqui eu acho interessante você mesmo olhar numa tabelinha dessas para se acostumar com esse tipo de tabela, mas de qualquer forma vou fornecer os dados importantes aqui:
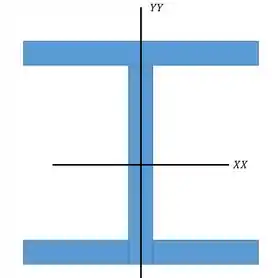
Gente, eu coloquei os dois momentos de inércia mas a gente só vai precisar de um, você lembra qual é?
O menor né!! Lembra que a flambagem é uma desgraçada e sempre vai atacar no pronto fraco da nossa coluna que é o menor momento de inércia. Dessa forma o momento de inércia que vamos utilizar é:
Passo 3
Agora é só substituir na equação da flambagem e achar a carga crítica:
Logo a máxima carga que a coluna consegue suportar sem sofrer flambagem é de .
Mas essa pode não ser a carga máxima porque essa coluna pode sofrer escoamento por compressão a uma carga de por exemplo...
Vamos conferir!
Passo 4
Para calcular a tensão de compressão vamos fazer:
Substituindo os valores vamos ter:
perceba que essa tensão é muito inferior à tensão de escoamento que é de .
Sendo assim a falha nessa estrutura ocorrerá primeiramente por flambagem. Isso talvez se explique pelo elevado comprimento da coluna (10 metros).
Passo 5
A maior carga admitida nessa configuração é de
Resposta
Ei, a resposta está no passo a passo :)