04. Determine uma representação paramétrica para a superfície que corresponde à porção do cilindro circular , situada entre os planos e .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema queremos obter a equação paramétrica da superfície do cilindro situada entre os planos e .
Tem alguma ideia do que podemos fazer? 🤔
Pelo que foi dito no enunciado temos uma simetria cilíndrica no problema, portanto podemos usar a parametrização por coordenadas cilíndricas que já conhecemos...
Nessa parametrização temos que substituir por e por onde é o raio do cilindro e é o ângulo que os pontos da superfície fazem com o semieixo positivo de ...
Lembra disso? 😉
Passo 2
Portanto, podemos escrever a equação paramétrica da superfície pelos dados que sabemos.
Como a equação do cilindro é dada por , podemos perceber que , ou seja ...
Dessa forma a equação paramétrica é dada por
Porém precisamos obter os valores que varia.
Se esboçarmos o cilindro e os planos no espaço, temos que
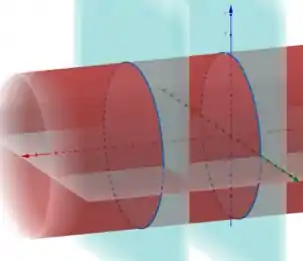
Portanto vemos que varia de a já que não h�� restrição em e de a ...
Logo, a parametrização da superfície será dada por
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍