Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Explícito

Ver Teoria
Exercício 612345789

Enunciado

UFRJ. Cálculo 2. 2C. 2022.1. Questão 1.

Seja f x , y = 3 x 2 - y 2 - 1 e S a superfície do gráfico de f x , y .

(a) Determine algebricamente e esboce o domínio de f x , y .

(b) Identifique e faça um esboço da curva de nível de f x , y que passa pelo ponto 3,0 .

(c) Identifique e esboce a superfície S .

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Essa questão é muito bacana! Temos uma função dada por f x , y = 3 x 2 - y 2 - 1 que descreve uma superfície S .

No item a) temos que determinar o domínio de f .

Já no item b) temos que esboçar a curva de nível que contém o ponto ( 3,0 ) .

Por fim, temos que esboçar a superfície no item c).

Lembra das definições de domínio e curvas de níveis? 🤔

Vamos imaginar uma fabrica de bolos, nessa fabrica entra farinha, chocolate, fermento, frutas e leite. E em uma fabrica de bolo o que sai são bolos, não é? 😋

Então podemos dizer que os ingredientes que entram na fábrica é o domínio e o bolo é a imagem desse domínio.

Ou seja, o domínio da função é tudo que podemos colocar na nossa função para que haja uma imagem.

Já a curva de nível de uma função é dada por tem a mesma altura k do plano x y . Lembra dos mapas topográficos de geografia? A ideia é muito parecida.

Depois dessa história do bolo fiquei com fome, mas vamos resolver esse exercício primeiro! 👀

Passo 2

Vamos encontrar o domínio de f primeiro.

Analisando a função, temos

f x , y = 3 x 2 - y 2 - 1

f ∈ R , logo o que está dentro da raiz deve ser positivo.

3 x 2 - y 2 - 1 ≥ 0

3 x 2 - y 2 ≥ 1

Com isso, vemos que

D o m f x , y = f x , y ∈ R 3 x 2 - y 2 ≥ 1

Certo?

Agora vamos esboçar a curva de nível que contém o ponto 3,0 .

Mas qual nível está esse ponto??

Se substituirmos o ponto em f x , y vamos encontrar seu valor em z e esse é exatamente o valor que procuramos, ou seja

f 3,0 = 3 3 2 - 0 2 - 1

f 3,0 = 26

Igualando a função f em 26 , temos

3 x 2 - y 2 - 1 = 26

Elevando os dois lados ao quadrado

3 x 2 - y 2 - 1 = 26

Simplificando a equação, temos

3 x 2 - y 2 = 2 7

Tranquilo até aqui?

Passo 3

Olhando a equação com mais atenção, vemos que ela se parece com algo familiar.

A equação da hipérbole não é dada por x 2 a 2 - y 2 b 2 = 1 ?

Podemos manipular essa equação para ficar com a mesma cara

3 x 2 - y 2 = 27

3 x 2 27 - y 2 27 = 1

x 2 9 - y 2 27 = 1

Esboçando o gráfico dessa hipérbole onde a 2 = 9 e b 2 = 27

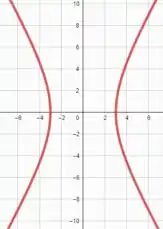
Agora o que resta é esboçar a superfície S , ou seja, f x , y = 3 x 2 - y 2 - 1  

Como as curvas de níveis de S são dados por

3 x 2 - y 2 = k + 1

Ou seja

x 2 k + 1 3 - y 2 k + 1 = 1

São hipérboles em que a 2 = k + 1 3 e b 2 = k + 1 . Podemos esboçar algumas curvas de níveis no espaço tridimensional e no fim, vamos chegar em uma superfície do tipo

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

a) D o m f x , y = f x , y ∈ R 3 x 2 - y 2 ≥ 1

b) x 2 9 - y 2 27 = 1

c) x 2 k + 1 3 - y 2 k + 1 = 1

Exercícios de Livros Relacionados

Identifique a superfície que tem a equação paramétrica dada. r → u , v = 2 s e nu i → + 3 c o s c o suj → + v k → , 0 ≤ v ≤ 2
Determine se os pontos P e Q estão na superfície dadavec r (u , v) = 〈u + v , u^2 - v , u + v^2〉 P (3 , - 1,5) , Q ( - 1,3 , 4 )
Determine se os pontos P e Q estão na superfície dadavec r (u , v) = 〈2 u + 3 v , 1 + 5 u - v , 2 + u + v〉 P (7,10,4) , Q ( 5,22,5 )
Identifique a superfície que tem a equação paramétrica dada. r s , t = ⟨ s , t , t 2 - s 2 ⟩
1 . Seja S uma superfície parametrizada por φ u , v = v cos ⁡ u ,v s e nu , 1 - v 2 0u2 π v ≥ 0 Identifique esta superfície. Esta superfície é regular ? Trace as curvas na superfice S. Definidas por φ