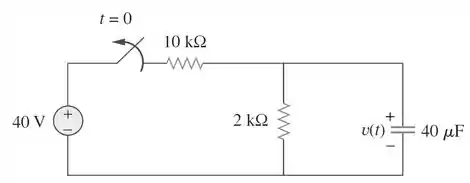
A chave do circuito abaixo foi fechada há um bom tempo e é aberta em . Determine para
Passo 1
O enunciado diz que a chave do circuito estava fechada há um bom tempo e que, posteriormente, foi aberta. Isso significa que o capacitor está totalmente carregado e isso faz com que ele tenha uma tensão diferente de zero em .
Passo 2
Então, vamos encontrar essa tensão em
Para isso, temos que lembrar que o capacitor em CC é um circuito aberto. Logo, podemos encontrar no circuito abaixo:
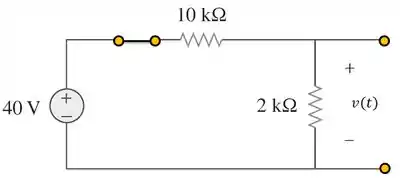
Aplicando divisor de tensão:
Em a chave está na iminência de abrir, mas ainda não abriu, e temos exatamente o circuito acima. Portanto:
Como a tensão no capacitor não pode variar instantaneamente:
Passo 3
Agora que já encontramos o valor da tensão no instante inicial, vamos encontra-la para .
Quando a chave é aberta, temos o circuito abaixo e toda a energia armazenada no capacitor vai começar a descarregar no resistor de .
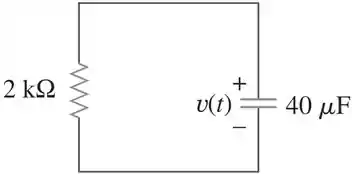
Como podemos ver, o circuito acima é o circuito RC sem fonte, e sabemos que a sua resposta natural será:
Calma, foi muito rápido? Vou relembra como chegamos nessa resposta.
Vamos desenhar as correntes:
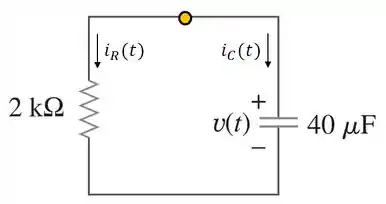
Agora, vamos aplicar a LCK no nó amarelo:
A gente sabe quais são as relações de corrente no capacitor e no resistor:
Substituindo:
Essa equação é uma EDO de primeira ordem. Você lembra como resolvê-la?
Para resolver essa equação, primeiro vamos obter a equação característica:
Sabemos que a solução geral da equação é dada por:
Sendo uma constante.
Substituindo o valor de encontrado, temos:
Viu só?
Agora, como e :
Passo 4
Para terminar, precisamos encontrar a constante . Para isso vamos utilizar a nossa condição inicial, pois em a chave acabou de se abrir:
Logo, a tensão no capacitor para será: