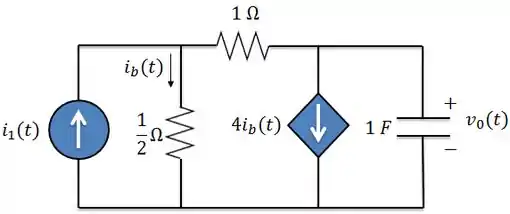
Determine a resposta ao degrau unitário e a resposta à rampa unitária do circuito abaixo.
Passo 1
O enunciado pede para a gente determinar a tensão no capacitor para quando a fonte de corrente for um degrau unitário e para a rampa unitária . Para encontrarmos uma relação entre e , vamos fazer uma análise nodal no circuito.
Passo 2
Então, vamos fazer a análise nodal do circuito abaixo:
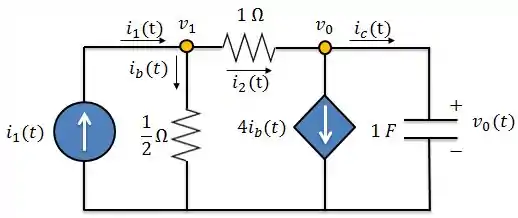
Aplicando LCK nos nós:
e
Escrevendo essas correntes em função das nossas tensões nodais, temos:
Substituindo esses valores nas equações nodais:
Simplificando:
Isolando na primeira equação e substituindo na segunda, obtemos:
Dando aquela ajeitada:
Como para o valor da corrente na fonte é igual a , temos:
Passo 3
Chegamos a EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.
Primeiro, vamos resolver a homogênea:
Para resolver essa equação, primeiro vamos obter a equação característica:
Logo a solução geral da equação é dada por:
Passo 4
Agora, precisamos encontrar a solução particular.
Como é uma constante, a solução particular deve ser também uma constante:
sendo B uma constante.
Substituindo, temos:
Como a derivada de uma constante é zero:
Portanto, a solução geral é:
Passo 5
Agora, precisamos encontrar o valor da constante Para isso, sempre usamos a nossa condição inicial.
O capacitor está inicialmente descarregado. Logo, para . Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo:
Que também podemos escrever assim:
Passo 6
Pronto, encontramos a resposta ao degrau unitário. Agora precisamos encontrar a resposta à rampa unitária. Sabemos que se a gente integrar a resposta ao degrau unitário, encontraremos a resposta à rampa unitária. Logo:
Que também podemos escrever assim:
Resposta
Quando
Quando