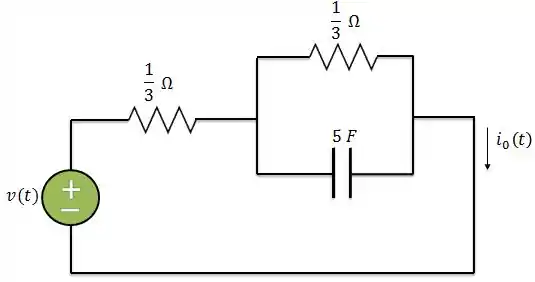
Determine se o circuito abaixo não contiver energia armazenada para , e se
Passo 1
O enunciado nos pede a corrente quando a tensão da fonte é o impulso unitário . Ou seja, quando tem a seguinte forma:
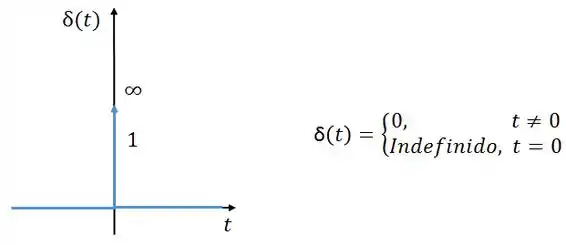
Passo 2
Primeiro, vamos analisar em . Como o impulso de tensão não pode ser aplicado no capacitor nem no resistor que está em paralelo com ele, porque causaria uma mudança repentina na tensão do capacitor.
Ele deve ser aplicado no primeiro resistor de , gerando um impulso de corrente:
Pronto, encontramos a corrente em .
Passo 3
Agora falta calcularmos para
Vamos distribuir a corrente como no circuito abaixo:
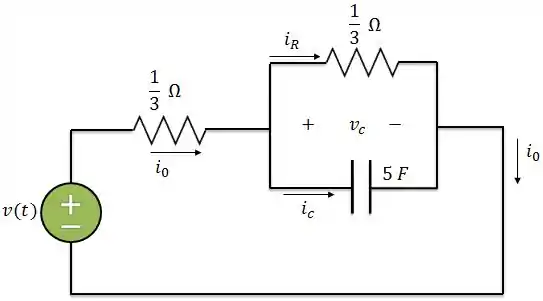
Aplicando a LCK, temos:
Como,
e
Substituindo:
Então, para encontrarmos para , precisamos encontrar antes para podermos substituir na equação aí de cima.
Passo 4
Agora, vamos aplicar a LTK no circuito:
Igualando as duas equações de a gente encontra:
Passo 5
Para a tensão da fonte é zero.
Vamos resolver a EDO homogênea aí de cima. Ela tem a seguinte equação característica:
Logo,
Passo 6
Precisamos encontrar a constante . Para isso, vamos analisar a tensão no capacitor no instante inicial
Lembra do impulso de corrente que falamos no início do exercício?
Então, esse impulso de corrente, ao chegar ao nó, deve circular apenas pelo capacitor, porque se alguma parcela dele passasse pelo resistor de que está em paralelo com o capacitor, causaria uma mudança repentina na tensão do capacitor.
Logo, o impulso de corrente passa pelo capacitor e de acordo com o teorema, um impulso de corrente passando pelo capacitor faz com que sua tensão instantaneamente suba para o valor do impulso multiplicado pelo inverso da capacitância.
Passo 7
Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo:
Passo 8
Agora que encontramos , podemos substituí-lo na equação abaixo para encontrarmos para
Simplificando:
Portanto:
Que também podemos escrever assim: