No circuito mostrado na figura abaixo
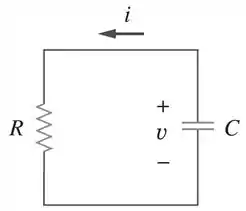
- Determine os valores de R e C
- Calcule a constante de tempo
- Determine o tempo necessário para a tensão cair para a metade do seu valor inicial em
Passo 1
A primeira coisa que se pede é pra calcular o valor de R e C no circuito. Se a gente observar, R e C estão em paralelo no circuito. Então, e acordo com a lei de Ohm:
Passo 2
Agora precisamos calcular o valor de C. Na teoria de circuitos RC chegamos à seguinte relação:
Como o enunciado nos disse que a tensão é:
Então:
Passo 3
Também na teoria de circuito RC, vimos que:
Passo 4
Quando a tensão vale:
Como pede o tempo para que a tensão caia à metade, então:
Aplicando aos dois lados da equação:
Resposta
- e
Exercícios de Livros Relacionados
Se o circuito está em regime permanente em t = 0 - , calcule v para t0 .
Supondo que a chave na figura 7.87 se encontra na posição A há um longo período e seja mudada para a posição B em t = 0 . Em seguida, tem t = 1s , a chave se move de B para C . Determine v c t para t
Projete um computador analógico para simular a seguinte equação: d 2 v d t 2 + 5 ⋅ v = - 2 ⋅ f t
Para o circuito da figura 7.88, se v = 10 ⋅ e - 4 tVei = 0.2 ⋅ e - 4 t , t0 a Determine R e C . b Determine a constante de tempo. c Calcule a energia inicial no capacitor. d Obtenha o tempo necessário
Uma ponta de prova de atenuação empregada em osciloscópios foi projetada para reduzir a magnitude da tensão de entrada vi por um fator 10. Conforme ilustrado na Figura 7.149, o osciloscópio possui res