Considerando a circuito da figura, composto de valores padrão:
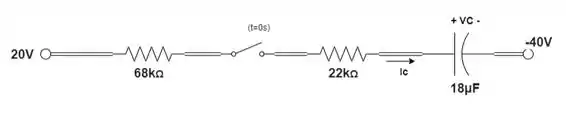
- Determine a constante de tempo do circuito.
- Escreva a equação matemática para a tensão depois qua chave é fechada.
- Escreva a expressão matemática para a corrente depois que a chave é fechada.
Passo 1
Para calcular a constante de tempo , vamos usar nossa conhecida fórmula:
Passo 2
Sabemos que após a chave for fechada, ocorre o carregamento do capacitor e sua tensão aumenta de acordo com a fórmula:
Passo 3
Para calcular a corrente após a chave fechar, seguimos a fórmula:
Resposta
a)
b)
c)