Considerando o circuito RC na figura composto por valores padrão:
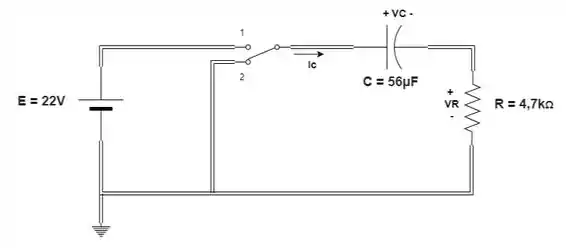
- Determine a constante de tempo do circuito quando a chave é colocada na posição 1.
- Determine a expressão matemática para a tensão entre os terminais do capacitor após a chave ter sido colocada na posição 1.
Passo 1
Vamos calcular a constante de tempo pedida no item a, como sabemos a fórmula é:
Passo 2
Sabemos que quando a chave é colocada na posição 1, o capacitor é carregado e sua tensão aumenta de acordo com a fórmula:
Resposta
Exercícios de Livros Relacionados
Se o circuito está em regime permanente em t = 0 - , calcule v para t0 .
Supondo que a chave na figura 7.87 se encontra na posição A há um longo período e seja mudada para a posição B em t = 0 . Em seguida, tem t = 1s , a chave se move de B para C . Determine v c t para t
Projete um computador analógico para simular a seguinte equação: d 2 v d t 2 + 5 ⋅ v = - 2 ⋅ f t
Para o circuito da figura 7.88, se v = 10 ⋅ e - 4 tVei = 0.2 ⋅ e - 4 t , t0 a Determine R e C . b Determine a constante de tempo. c Calcule a energia inicial no capacitor. d Obtenha o tempo necessário
Uma ponta de prova de atenuação empregada em osciloscópios foi projetada para reduzir a magnitude da tensão de entrada vi por um fator 10. Conforme ilustrado na Figura 7.149, o osciloscópio possui res