Considerando o circuito RC na figura composto por valores padrão:
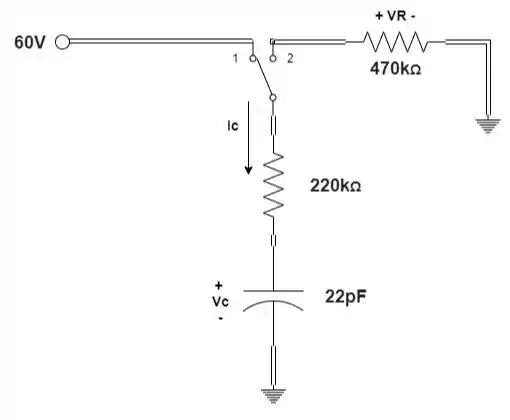
- Determine as expressões matemáticas para a tensão e a corrente em quando a chave é colocada na posição 1.
- Determine as expressões matemáticas para a tensão e a corrente se a chave for colocada na posição 2 a um tempo igual a cinco constantes de tempo do circuito de carga.
Passo 1
Primeiro vamos calcular a constante de tempo para a fase de carregamento:
Passo 2
Sabemos que a tensão do capacitor aumenta ao longo do tempo quando a chave está na posição 1, pois ele está sendo carregado:
Passo 3
Enquanto a tensão no capacitor aumenta, a corrente no capacitor diminui seguindo a equação:
Passo 4
Para calcular a resposta da letra b, temos que considerar que após 5 constantes de tempo, o capacitor está completamente carregado.
Logo quando a chave é colocada na posição 2, o capacitor irá descarregar a partir da tensão até 0V seguindo a equação:
Ao mesmo tempo que a corrente irá diminuir ao longo do tempo:
Passo 5
Mas temos que prestar atenção nesse detalhe aqui, como a corrente está definida no desenho no sentido para baixo:
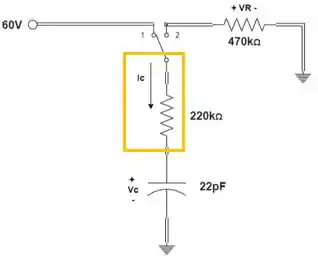
Quando a chave estiver na posição 2, o capacitor irá descarregar e a corrente irá circular no outro sentido (para cima), logo precisamos inverter o sentido de :
Passo 6
Porém devemos perceber que a constante de tempo , pois aumentamos a resistência do circuito:
Passo 7
Substituindo os valores nas fórmulas de descarregamento:
Resposta
a)
b)