Determine a tensão no capacitor para e no circuito abaixo:
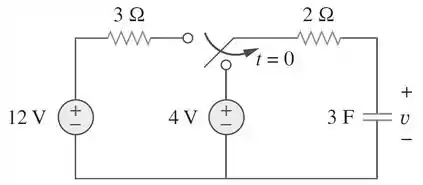
Passo 1
Vamos começar. Enquanto a chave está na posição horizontal, formando o seguinte circuito.
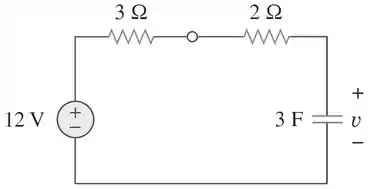
Como a chave estava nessa posição há um tempo suficiente para carregar totalmente o capacitor. Ele pode ser tratado como um circuito aberto.
Passo 2
Com isso, não terá circulação de corrente. Logo, não há queda de tensão nos resistores e a tensão no capacitor será a própria tensão da fonte.
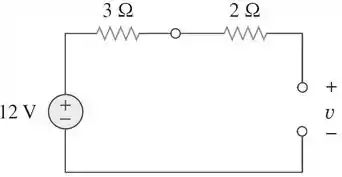
Passo 3
Em , a chave muda de posição e o circuito passa a ser assim:
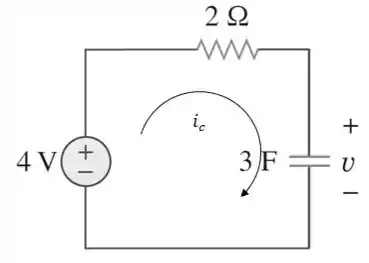
Aplicando a famosa LTK no circuito:
Como,
Substituindo:
Passo 4
Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.
Primeiro, vamos resolver a homogênea:
Para resolver essa equação, primeiro vamos obter a equação característica:
Logo a solução geral da equação é dada por:
Passo 5
Agora, precisamos encontrar a solução particular.
Como é uma constante, a solução particular deve ser também uma constante:
sendo B uma constante.
Substituindo, temos:
Como a derivada de uma constante é zero:
Portanto, a solução geral é:
Passo 6
Agora, precisamos encontrar o valor da constante Para isso, sempre usamos a nossa condição inicial.
Quando a chave ainda estava na posição horizontal, mas estava na iminência de se mover, temos o instante . Nesse instante, como vimos, o capacitor está totalmente carregado.
Logo, . Lembrando que a tensão no capacitor não pode variar instantaneamente, então:
Portanto, de acordo com a nossa condição inicial, temos:
Substituindo: