Uma linha de transmissão trifásica de tem impedância de por fase. Se ela alimentar uma carga de com fator de potência (atrasado), determine:
A potência complexa.
A perda de potência na linha.
A tensão na entrada da linha.
Passo 1
Vamos considerar que a tensão fornecida pelo enunciado é a tensão de fase na carga, ou seja:
Além disso, o enunciado nos forneceu a potência aparente na carga e o fator de potência.
Como o fator de potência é atrasado a carga é predominantemente indutiva e o ângulo do fator de potência é positivo, logo:
Passo 2
Na letra , temos que calcular a potência complexa, sabemos que uma das fórmulas de potência complexa é:
Então, substituindo pelos valores:
Passando para forma retangular temos:
Passo 3
Agora, vamos analisar uma fase da linha de transmissão. Se liga no esquema abaixo:
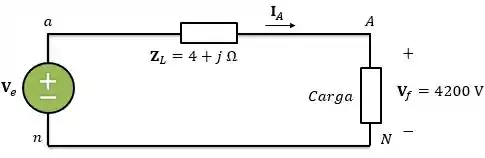
Na letra , nosso objetivo é calcular as perdas de potência na linha. Para isso, temos que saber que as perdas na linha estão relacionadas à parcela resistiva da impedância de linha, ou seja:
Logo, precisamos encontrar o módulo da corrente . Para isso, vamos usar o valor que encontramos para a potência complexa e a fórmula abaixo:
Logo,
Agora é só substituir na formula da potência:
Passo 4
Para terminar, precisamos calcular a tensão de entrada da linha, ou seja, o do esquema abaixo:
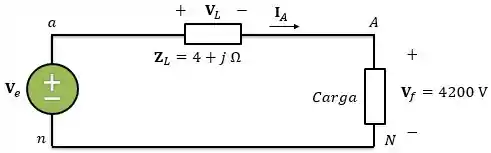
Aplicando a lei das tensões de Kirchhoff na malha do circuito, temos:
Pela lei de Ohm:
Logo,