A potência total medida em um sistema trifásico que alimenta uma carga conectada em estrela equilibrada é de 12 kW com fator de potência 0,6 (adiantado). Se a tensão de linha for 208 V, calcule a corrente de linha e a impedância de carga .
Passo 1
O enunciado nos disse qual a potência ativa que alimenta a carga:
Além disso, o enunciado nos forneceu o fator de potência e a tensão de linha.
Como o fator de potência é adiantado a carga é predominantemente capacitiva e o ângulo do fator de potência é negativo, logo:
Passo 2
Para encontrar a corrente de linha, primeiro temos que calcular a potência complexa, sabemos que uma das fórmulas de potência complexa é:
Pelo triângulo das potências, temos que:
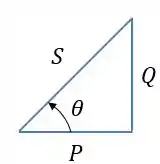
Então, substituindo pelos valores, a potência complexa trifásica será:
Passo 3
Agora, vamos utilizar a seguinte fórmula de potência complexa:
Logo,
Substituindo os valores que temos:
Passo 4
Para calcularmos a impedância de carga , vamos partir de uma outra formula de potência complexa trifásica:
Pela lei de Ohm, a tensão na carga será:
Substituindo na fórmula da potência, temos:
Como :
Além disso, como a carga está conectada em estrela:
Logo, a impedância da carga será:
Passando para forma retangular: