Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos Trifásicos

Ver Teoria
Exercício 10123456789

Enunciado

Obtenha as correntes de linha no circuito trifásico abaixo:

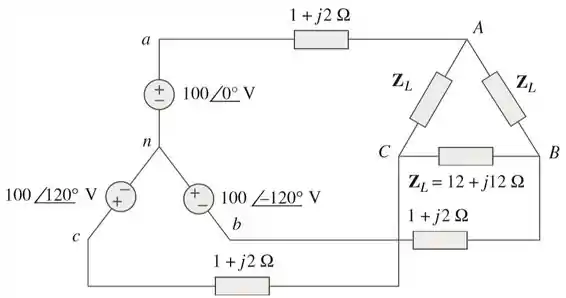
Passo 1

Para evitar cruzar linhas no circuito e ficar mais fácil de analisar, vamos redesenhar:

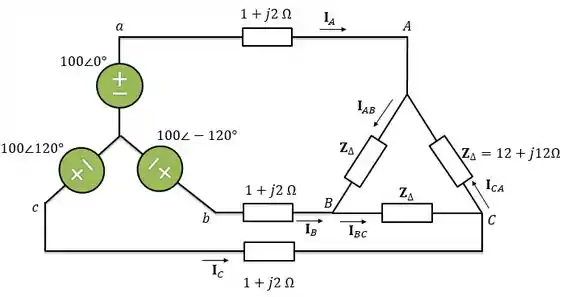
Passo 2

A primeira coisa que teremos que fazer é transformar a carga que está ligada em delta para um estrela. A gente faz isso porque fica mais fácil de analisar e calcular as correntes de linha.

Então, precisamos lembrar da relação de transformação de impedância de delta para estrela:

Z ∆ = 3 Z Y

Logo, as impedâncias da carga em estrela serão:

Z Y = 12 + j 12 3

Z Y = 4 + j 4

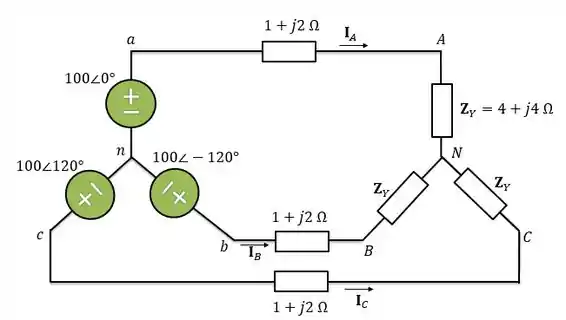
Passo 3

Como o circuito é equilibrado, podemos analisar uma das fases para achar a corrente de linha do circuito e depois defasar as outras de 120 ° . Então:

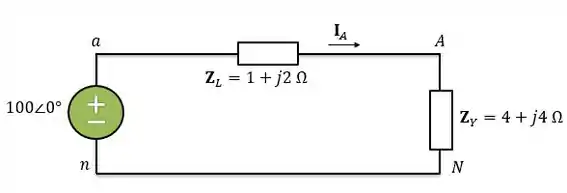
Pela lei de Ohm, a corrente de linha na fase a será:

I A = 100 ∠ 0 ° Z L + Z Y

I A = 100 ∠ 0 ° 1 + j 2 + 4 + j 4

I A = 100 ∠ 0 ° 5 + j 6

I A = 100 ∠ 0 ° 7,81 ∠ 50,19 °

I A = 12,8 ∠ - 50,19 °   A

Passo 4

Lembrando que a sequência de fase do exercício é a b c . Então, para as fases b e c teremos as seguintes correntes:

I B = I A ∠ - 120 °

I B = 12,8 ∠ - 50,19 ° - 120 °

I B = 12,8 ∠ - 170,19 °   A

I C = I A ∠ + 120 °

I C = 12,8 ∠ - 50,19 ° + 120 °

I C = 12,8 ∠ 69,81 °   A

Resposta

I A = 12,8 ∠ - 50,19 °   A

I B = 12,8 ∠ - 170,19 °   A

I C = 12,8 ∠ 69,81 °   A

Exercícios de Livros Relacionados

Se V a n=220 ∠60 °V no circuito da Figura 12.49, determine, para a carga, as corrente de fase I A B ,I B CeI C A .
Três cargas trifásicas associadas em paralelo são alimentadas por uma fonte trifásica equilibrada:Carga 1: 250 kVA, FP = 0,8 (atrasado)Carga 2: 300 kVA, FP = 0,95 (adiantado)Carga 3: 450 kVA, FP unitá
No sistema trifásico estrela-triângulo equilibrado da Figura 12.46 , determine a corrente de linha I L e a potência média liberada para a carga.
Um sistema quadrifilar estrela-estrela equilibrado apresenta as seguintes tensões de fase V a n = 120 ∠ 0 ° ,V b n = 120 ∠ - 120 ° ,V c n = 120 ∠ 120 ° A impedância de carga por fase é 19 + j 13Ω e a
Considere a Figura 12.51 e elabore um problema para ajudar outros estudantes a entender melhor os circuitos conectados em triângulo-triângulo equilibrado.