Obtenha as correntes de linha no circuito trifásico da figura
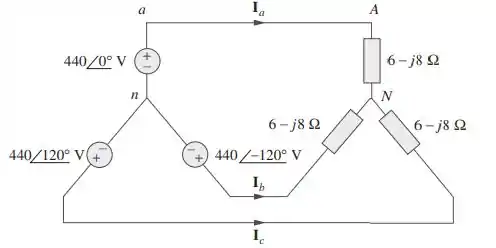
Passo 1
Esse exercício assusta de primeira mas é bem simples se analisarmos cada fase!
Perceba que o sistema é um sistema Y-Y BALANCEADO, ou seja, todas as impedâncias são iguais e as tensões também (o que muda é o ângulo de fase pra fase).
Por isso, podemos analisar uma fase só (digamos, fase A), e analisar a partir daí.
Vamos primeiro desenhar somente uma fase e fazer o que chamamos de equivalente monofásico do sistema (isso cai muito em prova).
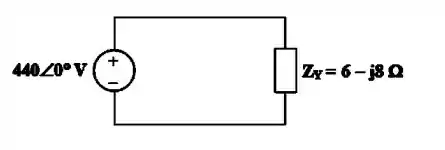
Passo 2
Agora, vamos calcular a corrente desse sistema monofásico (que é a fase A)
Daí achamos a corrente e .
Note que, estamos trabalhando com sequência positiva ABC já que podemos ver claramente na figura que é essa a sequência.
Resposta
Exercícios de Livros Relacionados
Se V a n=220 ∠60 °V no circuito da Figura 12.49, determine, para a carga, as corrente de fase I A B ,I B CeI C A .
Três cargas trifásicas associadas em paralelo são alimentadas por uma fonte trifásica equilibrada:Carga 1: 250 kVA, FP = 0,8 (atrasado)Carga 2: 300 kVA, FP = 0,95 (adiantado)Carga 3: 450 kVA, FP unitá
No sistema trifásico estrela-triângulo equilibrado da Figura 12.46 , determine a corrente de linha I L e a potência média liberada para a carga.
Um sistema quadrifilar estrela-estrela equilibrado apresenta as seguintes tensões de fase V a n = 120 ∠ 0 ° ,V b n = 120 ∠ - 120 ° ,V c n = 120 ∠ 120 ° A impedância de carga por fase é 19 + j 13Ω e a
Considere a Figura 12.51 e elabore um problema para ajudar outros estudantes a entender melhor os circuitos conectados em triângulo-triângulo equilibrado.