Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos Trifásicos

Ver Teoria
Exercício 21345678910

Enunciado

Em um sistema trifásico estrela-estrela equilibrado, a fonte é uma sequência a b c de tensões e V a n = 100 ∠ 20 °   V RMS. A impedância de linha por fase é   0,6 + j 1,2   Ω , enquanto a impedância por fase da carga é 10 + j 14   Ω . Calcule as correntes de linha e as tensões de carga.

Passo 1

Enunciado diz que a fonte está em estrela e é equilibrada e ainda fornece o valor da tensão da fase a . Além disso, ele diz que a sequência é a b c . Logo, já sabemos o valor das tensões das fases b e c :

V b n =   V a n ∠ - 120 °

V b n =   100 ∠ 20 ° - 120 °

V b n =   100 ∠ - 100 °   V

V c n =   V a n ∠ + 120 °

V c n =   100 ∠ 20 ° + 120 °

V c n =   100 ∠ + 1 40 °   V

Montei o circuito abaixo para ficar mais fácil de visualizar:

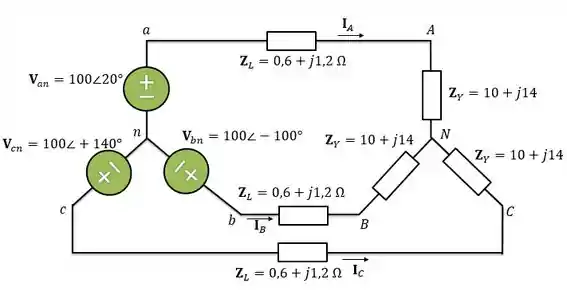
Passo 2

Agora, vamos calcular as correntes de linha. Como o circuito é equilibrado, podemos analisar somente uma das fases e depois defasar as outras de 120 ° .

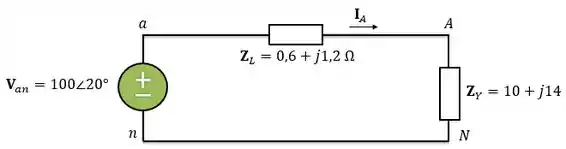
Analisando o circuito acima, temos que:

I A = V a n Z L + Z Y

I A = 100 ∠ 20 ° 0,6 + j 1,2 + 10 + j 14

I A = 100 ∠ 20 ° 10,6 + j 15,2

I A = 100 ∠ 20 ° 18,53 ∠ 55,12 °

I A = 5,396 ∠ - 35,12 °   A

Passo 3

Agora vamos calcular as outras correntes de linha. Lembrando que a sequência é a b c .

I B = I A ∠ - 120 °

I B = 5,396 ∠ - 35,12 ° - 120 °

I B = 5,396 ∠ - 155,12 °   A

I C = I A ∠ + 120 °

I C = 5,396 ∠ - 35,12 ° + 120 °

I C = 5,396 ∠ 84,88 °   A

Passo 4

O que falta calcular são as tensões na carga. Pela Lei de Ohm:

V Z L A = Z Y I A

V Z L A = 10 + j 14 × 5,396 ∠ - 35,12 °  

V Z L A = 17,2 ∠ 54,46 °   × 5,396 ∠ - 35,12 °  

V Z L A = 92,84 ∠ 19,34 °   A

V Z L B = Z Y I B

V Z L B = 10 + j 14 × 5,396 ∠ - 155,12 °  

V Z B = 17,2 ∠ 54,46 °   × 5,396 ∠ - 155,12 °  

V Z L B = 92,84 ∠ - 100,36 °   A

V Z L C = Z Y I C

V Z L C = 10 + j 14 × 5,396 ∠ 84,88 °   °  

V Z C = 17,2 ∠ 54,46 °   × 5,396 ∠ 84,88 °  

V Z L C = 92,84 ∠ 139,34 °   A

Também poderíamos ter feito essa questão calculando o valor da tensão em somente uma fase e depois defasar as outras de 120 ° .

Resposta

I A = 5,396 ∠ - 35,12 °   A

I B = 5,396 ∠ - 155,12 °   A

I C = 5,396 ∠ 84,88 °   A

V Z L A = 92,84 ∠ 19,34 °   A

V Z L B = 92,84 ∠ - 100,36 °   A

V Z L C = 92,84 ∠ 139,34 °   A

Exercícios de Livros Relacionados

Se V a n=220 ∠60 °V no circuito da Figura 12.49, determine, para a carga, as corrente de fase I A B ,I B CeI C A .
Três cargas trifásicas associadas em paralelo são alimentadas por uma fonte trifásica equilibrada:Carga 1: 250 kVA, FP = 0,8 (atrasado)Carga 2: 300 kVA, FP = 0,95 (adiantado)Carga 3: 450 kVA, FP unitá
No sistema trifásico estrela-triângulo equilibrado da Figura 12.46 , determine a corrente de linha I L e a potência média liberada para a carga.
Um sistema quadrifilar estrela-estrela equilibrado apresenta as seguintes tensões de fase V a n = 120 ∠ 0 ° ,V b n = 120 ∠ - 120 ° ,V c n = 120 ∠ 120 ° A impedância de carga por fase é 19 + j 13Ω e a
Considere a Figura 12.51 e elabore um problema para ajudar outros estudantes a entender melhor os circuitos conectados em triângulo-triângulo equilibrado.