A matriz é simétrica com autovalores , e . Sabemos que e são autovetores de .
(b) Determine uma decomposição espectral de .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Para essa questão foi dado algumas informações sobre a matriz a como por exemplo temos três autovalores , e , foi dado também dois autovetores e e no item anterior calculamos mais um autovetor, onde encontramos o autovetor associado ao autovalor , .
O objetivo principal dessa questão é calculado decomposição espectral da matriz .
Mas você sabe o que significa decomposição espectral de uma matriz?
A decomposição espectral de uma matriz é uma forma de se escrever a matriz através equação
Onde é uma matriz composta pelos autovetores escritos na forma unitária da matriz e a matriz é uma matriz composta pelos autovalores da matriz em sua diagonal principal.
Com essas ideias em mente podemos partir para os cálculos!
Passo 2
Como dito anteriormente a decomposição espectral segue a equação
Primeiro vamos montar as matrizes e .
A matriz é formada pelos autovetores unitários da matriz onde para se obter um vetor unitário devemos dividi-lo pela sua norma, ou seja
Se , e , logo
Para
Para
Substituindo esses vetores da matriz , temos
Aproveitando que acabamos de definir a matriz , a matriz transposta será
Lembrando que para transformar uma matriz em uma matriz transposta devemos converter o que é linha em coluna e a coluna em linha, como se espetássemos a diagonal principal da matriz e rotacionasse 180°.
Parar definir a matriz devemos seguir uma formulinha, onde
A diagonal principal da matriz é formada pelos autovalores associados à matriz , os quais foram dados do enunciado, onde , e , portanto
Passo 3
Já temos todas as ferramentas necessárias para montar a nossa equação, que terá o seguinte aspecto
Resolvendo essas operações, temos
Continuando o produto das matrizes, para facilitar a visualização, vamos calcular uma coluna de cada vez.
Passo 4
Para a coluna 1:
Para a coluna 2:
Para a última coluna:
Passo 5
Encontramos a matriz que podemos observar sua simetria, onde uma matriz deve seguir
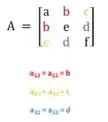
Da mesma forma da matriz
Foi um pouco trabalhoso, não é? Mas tenho certeza que valeu o esforço!

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍