Abaixo temos uma peça com 4 seções diferentes. Sabendo que ela foi sujeita a uma carga P de intensidade desconhecida e que possui , determine o máximo valor de P para que essa barra apenas sofra deformações elásticas, ou seja, fique na iminência de entrar no regime plástico.
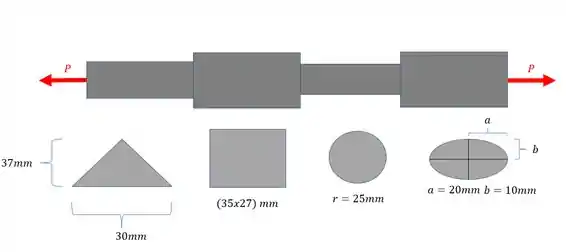
Passo 1
Nesse tipo de questão podemos ficar tranquilo quanto o cálculo que iremos fazer. Sabemos que devemos fazer uma igualdade de tensões, nesse caso igualando a tensão de escoamento com a maior tensão entre as duas seções, fazemos isso pois assim acharemos uma relação entre a carga que estamos aplicando e a tensão que fará a nossa barra deformar plasticamente. Mas aí surgem duas dúvidas.
A primeira é saber qual seção produz maior tensão, e a segunda é como trabalharemos unidades e valores, para isso temos que tomar alguns cuidados.
Passo 2
O primeiro problema é fácil solucionar, basta olharmos a fórmula de tensão normal.
Basta analisarmos o seguinte, se aumentamos a área, diminuímos a tensão e se diminuímos a área aumentamos a tensão. Ou seja, basta calcularmos as áreas e a que for menor será a que produzira maiores tensões. Sendo assim teremos que
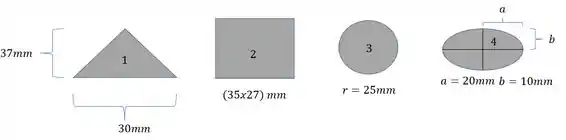
Então sabemos que devemos usar a .
Outra coisa que podemos ver é que o normal que age na nossa peça é a própria carga P, logo teremos que
E por fim como queremos o valor máximo de P sem que haja deformações permanentes na peça, faremos
Passo 3
Agora que já temos todos os valores, devemos adequar as unidades, sabemos que
Sabemos também que a nossa área é
Ou seja, acharemos a nossa força em Newtons nesse caso, substituindo na fórmula teremos que