Verifique se o problema abaixo apresenta tensões residuais. Caso apresente determine o valor delas.
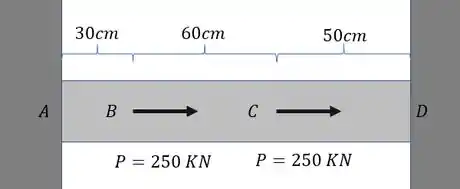
Passo 1
Sabemos que para sabermos quais tensões agem na nossa peça, precisamos determinar os normais que estão agindo nela, faremos esse exercício das duas formas que aprendemos, primeiro pelo método mais longo, e depois conferiremos a reposta pelo método mais curto.
Sabemos que o método mais longo passa por 4 etapas que são
Primeiro calcularemos as tensões na peça fingindo que ela se comporta elasticamente.
Em segundo conferimos se em algum ponto da peça a tensão calculada é maior que a tensão de escoamento, e caso seja modificamos a nossa conta.
Em terceiro lugar calculamos as deformações plásticas.
E por fim calculamos as tensões residuais.
Para o método mais rápido sabemos que apenas os passos 1 e 2 já resolvem o nosso problema. Mas antes de fazermos essa analise precisamos conhecer os esforços na barra.
Passo 2
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá
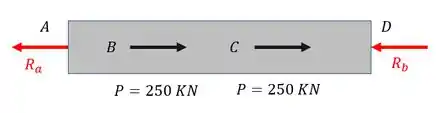
Fazendo o somatório de forças teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 3
Temos que lembrar que a nossa equação de compatibilidade terá como fórmula a nossa equação de deformação total, dada por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação, ou seja, a deformação da nossa barra deve ser igual a deformação total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto a área quanto o módulo de elasticidade são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Então o que falta é apenas determinar o valor dos normais.
Passo 4
Como só falta determinar o normal, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro normal do trecho AB
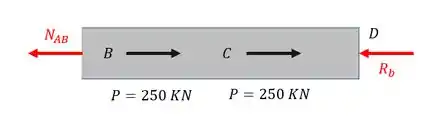
Fazendo o equilíbrio teremos que
Normal do trecho BC
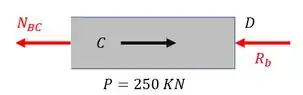
Fazendo o equilíbrio teremos que
Normal do trecho CD
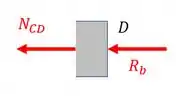
Fazendo o equilíbrio teremos que
Passo 5
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos cortar
Isolando teremos que
Agora é só calcularmos o valor de
Passo 6
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de
Passo 7
Agora que já sabemos a força em cada trecho, precisamos analisar as respectivas tensões, para isso temos que usar a nossa fórmula
Sabemos que
E a nossa área é
Sabendo todos os valores temos que lembrar que
Logo teremos que as tensões serão.
Como a nossa tensão de escoamento é podemos ver que apenas a tensão do trecho AB ultrapassa a tensão de escoamento, ou seja, todos os outros dois trechos sofreram deformações elásticas, mas o trecho AB sofrerá também deformações plásticas.
Passo 8
Como o trecho AB ultrapassou a tensão de escoamento, definimos que a tensão que calculamos é impossível e redefinimos ela como a tensão de escoamento, assim teremos que
Recalculado o normal teremos que
Mas também sabemos que, então recalculando o valor de teremos que
Esses valores devem ser guardados pois iremos usa-los novamente mais pra frente nos nossos cálculos.
Passo 9
Agora que sabemos que o trecho AB irá sofrer deformações plásticas iremos usar isso na nossa equação de compatibilidade, sabemos que
Iremos reescrever a nossa equação como
Já sabemos a fórmula que usamos para calcular as parcelas elásticas, e elas são dadas abaixo
Substituindo os nossos normais teremos que
E agora entra o maior cuidado que você deve tomar nessa questão, todos os dos normais será trocado pelo novo valor de que calculamos, não devemos de maneira nenhuma usar o primeiro valor que calculamos, mas sim o corrigido.
Com isso usaremos
Substituindo por enquanto só o valor de teremos
Vamos deixar essa equação parada por enquanto.
Passo 10
Como já sabemos que essa peça terá deformações plásticas, podemos determinar as tensões residuais que essa peça terá quando retirarmos o carregamento. Olhando o nosso diagrama de corpo livre teremos que

Sabemos que nesse caso a reação R produzira a seguinte tensão
E também produzirá a seguinte deformação
Que podemos reescrever como
Em que essa tensão é exatamente a nossa tensão residual.
Também podemos escrever a nossa equação de compatibilidade como
Com isso podemos escrever que
Com isso temos duas fórmulas para deformação plástica
Juntando as duas temos que
Podemos cortar o valor de E de todas as parcelas e isolar o valor da tensão
Isolando a nossa tensão teremos que
Sabemos que
Substituindo
Passo 11
Também disse que iria conferir a resposta através do cálculo mais rápido que já apendemos, para isso devemos lembrar que a nossa fórmula é
Em que é a primeira tensão que calculamos, considerando tudo lindo e sem deformações plásticas, e é a tensão real que definimos logo após descobrirmos que havia deformações plásticas, pra ser mais direto, a nossa própria tensão de escoamento, dessa forma teremos que
Fazendo o cálculo teremos que
Ou seja, realmente calculamos tudo coretinho sem termos nenhuma contradição.
Resposta
Ocorrem tensões residuais devido as deformações plásticas.