A prensa hidráulica abaixo é utilizada para comprimir o corpo de prova, que possui uma área de seção transversal , um comprimento inicial e um comportamento elastoplástico com e .
Se a prensa causa no corpo de prova uma variação de comprimento máxima , determine quais foram as variações de comprimento elástica e plástica sofridas pelo corpo de prova.
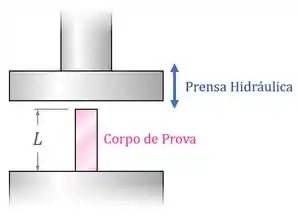
Passo 1
O que está acontecendo?
O corpo de prova se comporta de forma elastoplástica com um módulo de elasticidade e um limite de resistência ao escoamento .
Além disso, ele tem um comprimento inicial .
A prensa hidráulica vai comprimir esse corpo de prova, gerando nele uma variação de comprimento máxima .
Essa variação de comprimento máxima é composta por:
- Uma variação de comprimento elástica , que segue a Lei de Hooke, e ocorre até que a tensão no material alcance a tensão de escoamento ;
- E uma variação de comprimento plástica , que ocorre depois da tensão no material ter alcançado .
Ou seja, caso a tensão no material alcance , a variação de comprimento máxima vai ser:
E o que é que o exercício quer?
Ele quer que a gente calcule os valores de e .
Primeiro, devemos calcular o valor máximo da variação de comprimento elástica , que é o valor que ocorre quando a tensão no material é igual à .
Se essa variação elástica máxima for maior ou igual à variação de comprimento máxima no material, então toda a variação sofrida vai ter sido elástica.
Mas se essa variação elástica máxima for menor que , então a diferença será a variação de comprimento plástica .
Passo 2
Vamos começar calculando o valor máximo possível para !
O valor máximo da variação de comprimento elástica é aquele que ocorre quando a tensão no material é igual à , então vamos aplicar essa condição:
Mas, da Lei de Hooke, temos que , onde é a deformação elástica sofrida pelo material. Então:
Se é a deformação elástica sofrida pelo material, então é igual à variação de comprimento elástica sofrida dividida pelo comprimento da peça:
Assim, encontramos que:
Substituindo os valores:
- ;
- ;
- & ,
Encontramos que:
Passo 3
Agora vamos pensar...
Encontramos que o valor máximo possível para é , o que é muito menor que a variação de comprimento máxima sofrida pelo nosso corpo de prova.
Então o que aconteceu foi que:
- A tensão de escoamento foi atingida na peça;
- Por causa disso, a peça sofreu uma variação de comprimento elástica ;
- E também por causa disso, a peça começou a se comportar plasticamente, o que significa que todo o restante da variação de comprimento sofrida foi plástica.
Sabendo disso, já podemos calcular a variação de comprimento plástica na peça:
Substituindo e , encontramos que:
E assim finalizamos nosso exercício!