O comportamento da barra de alumínio abaixo pode ser considerado elastoplástico com e . Determine qual é a força necessária para fazer essa barra começar a se deformar plasticamente.
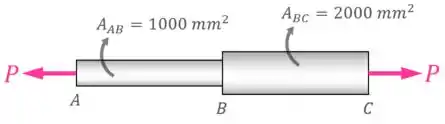
As áreas das seções transversais dos trechos e da barra são fornecidas na imagem.
Passo 1
O que está acontecendo?
As forças de tração geram ao longo de toda a barra uma força interna normal .
Essa força normal gera, nos trechos e da barra, tensões normais médias :
Onde e são as áreas das seções transversais dos trechos e da barra.
Para que a barra se deforme plasticamente, só é necessário que um dos seus trechos se deforme plasticamente.
E para que um trecho da barra se deforme plasticamente, é necessário que a tensão normal nesse trecho alcance o limite de resistência ao escoamento do material.
Para uma mesma força , o trecho que irá atingir essa tensão primeiro vai ser o trecho com a menor área de seção transversal . (No nosso caso, o trecho !)
E o que é que o exercício quer?
Ele quer saber qual é a força necessária para fazer a barra se deformar plasticamente.
(Ou seja, a força necessária para fazer um dos trechos da barra se deformar plasticamente.)
Passo 2
Então vamos lá!
A barra vai se deformar plasticamente primeiro no trecho , que possui uma área de seção transversal menor.
Então a força necessária para fazer a barra se deformar plasticamente é a força que faz com que a tensão em , , seja igual à tensão de escoamento :
Aplicando a fórmula da tensão normal média para o trecho , vamos ter:
Como a única força atuante na barra é a tração , a força interna normal na barra vai ser igual à .
Dessa forma, temos que:
Isolando , temos:
Substituindo os valores:
- ;
- & ,
Vamos encontrar que:
Como esse número é um pouco grande, podemos reescrevê-lo em :
Ou seja, precisamos de uma força para fazer a barra começar a se deformar plasticamente!