A barra tem área de seção transversal de . Se uma força for aplicada em e, então, removida, determine a tensão residual nas seções e .
Dados: .

Passo 1
O que está acontecendo?
A barra tem uma área de seção transversal e é feita de um material com um limite de resistência ao escoamento .
Ela é dividida nos trechos , de comprimento , e , de comprimento por uma força .
E ela é apoiada por forças de reação e nos apoios em e em , como mostra o seu diagrama de corpo livre:
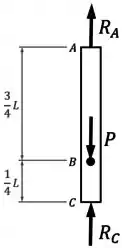
Como esses apoios em e em são fixos, eles garantem que a variação de comprimento total na barra seja sempre igual à zero:
E o que é que o exercício quer?
Ele quer saber a tensão residual nas seções e da barra quando a força é retirada.
Para que essa tensão residual exista, é necessário que o carregamento original da barra tenha gerado nela alguma variação de comprimento plástica/permanente .
Então vamos:
1. Analisar a barra em sua situação inicial para descobrirmos se vai haver alguma variação de comprimento permanente nela.
Para tanto, devemos:
- Considerar que não vai haver deformação plástica;
- E calcular as tensões nos trechos e da barra, verificando se elas vão ultrapassar ou não a resistência ao escoamento .
Se a tensão em um trecho ultrapassar , então vai haver deformação plástica.
Nesse caso, vamos ter que:
2. Adicionar a deformação plástica à nossa análise e definir .
E, por último, vamos:
3. Analisar a barra em sua situação final para descobrirmos qual é a tensão residual correspondente à variação de comprimento plástica gerada.
Passo 2
Então vamos começar avaliando a barra considerando que não vai haver deformação plástica.
Primeiro, observando o diagrama de corpo livre da barra...
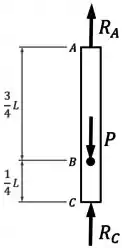
...e aplicando o equilíbrio de forças na vertical:
...encontramos que:
Em seguida, fazendo uma análise dos esforços internos na barra, vamos ter que:
Para as seções entre e ...
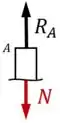
...o equilíbrio de forças requer que:
Mas como , isso significa que:
Já para as seções entre e ...
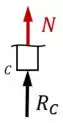
...o equilíbrio de forças requer que:
Por fim, a última análise que podemos fazer é encontrar uma equação de compatibilidade para a barra.
Por um lado, temos que a variação de comprimento total da barra deve ser igual à zero por causa dos apoios fixos:
Do outro, temos que a variação de comprimento total da barra é a soma das variações de comprimento dos trechos e .
Dessa forma, temos que:
Agora, como estamos considerando que não vai haver deformação plástica, podemos dizer que essas variações de comprimento e podem ser dadas pela fórmula:
Aplicando essa fórmula para e , a nossa equação de compatibilidade fica assim:
Multiplicando tudo por , temos que:
Em seguida, substituindo...
- Os comprimentos e ;
- & as forças normais e ,
...temos que:
Multiplicando tudo por , isso fica assim:
Fazendo as multiplicações, temos que:
E, finalmente, isolando , encontramos que:
E como , isso significa que:
Passo 3
Já analisamos toda a barra considerando que não vai haver deformação plástica.
Então agora podemos calcular quais seriam as tensões nos trechos e nesse caso.
Aplicando a fórmula da tensão normal média para o trecho , temos:
Substituindo , isso fica assim:
Em seguida, substituindo...
- ;
- ;
- & ,
...e prestando atenção nas unidades, encontramos que:
O que é menor que a tensão de escoamento .
Ou seja, o trecho da barra não vai sofrer deformação plástica.
Já aplicando a fórmula da tensão normal média para o trecho , temos:
Substituindo , temos:
E em seguida, substituindo e , encontramos que:
Vemos que a intensidade de é maior que a tensão de escoamento .
Então o trecho vai sofrer deformação plástica e a tensão que vai ocorrer efetivamente nele vai ser .
Isso significa que a força também não vai chegar a ser igual à .
Pegando a expressão:
Isolando :
E substituindo e , encontramos que efetivamente, o valor de vai ser:
Dica: Na hora da prova, destaque esses novos valores com uma caixa “novos valores” ou algo parecido. Assim você não se esquece deles!
Passo 4
Agora que sabemos que o trecho vai sofrer deformação plástica, podemos adicionar essa informação à nossa análise.
A equação de compatibilidade que antes era assim...
...agora vai levar em consideração que:
- A variação de comprimento do trecho só tem uma parcela elástica ;
- E que a variação de comprimento de tem uma parcela elástica e uma parcela plástica .
Dessa forma, a equação de compatibilidade vai ficar assim:
Aqui, como as variações de comprimento e são elásticas, podemos aplicar a fórmula para elas:
Substituindo essas expressões, a equação de compatibilidade fica assim:
Isolando , temos:
Substituindo , , e isso fica assim:
Colocando em evidência, temos:
E, finalmente, simplificando, isso fica assim:
Não precisamos realmente calcular , então vamos só guardar essa expressão para depois.
Passo 5
Agora que já sabemos que a peça vai sofrer uma deformação plástica , podemos ver que tensão residual essa deformação plástica vai gerar depois que a força for retirada.
Quando a força for retirada, o diagrama de corpo livre da barra vai ficar assim:
![]()
Essas reações só existem para compensar a deformação plástica e garantir que a variação de comprimento total na barra seja igual à zero.
Elas fazem isso gerando, ao longo de toda a barra:
- Uma força interna normal , e, consequentemente, uma tensão normal média ;
- E uma variação de comprimento .
Superpondo a variação de comprimento plástica com essa variação de comprimento causada pelas reações , temos a variação de comprimento total:
Impondo a condição , isso significa que:
Substituindo e a expressão encontrada no passo anterior para , temos:
Cortando com e com , encontramos a tensão residual que vai aparecer ao longo de toda a barra por causa da deformação plástica ocorrida:
Finalmente, substituindo...
- ;
- O novo valor encontrado para no Passo 3, ;
- & ,
...encontramos que a tensão residual ao longo de toda a barra (ou seja, tanto no trecho quando no trecho ) vai ser:
Como esse número é muito pequeno, podemos reescrevê-lo em na hora de fornecermos a nossa resposta: