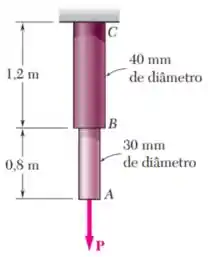
A barra consiste em duas partes cilíndricas e ; ela é feita de um aço doce considerado elastoplástico com e . Uma força é aplicada à barra e em seguida removida para dar a ela uma deformação permanente . Determine o valor máximo da força e o valor máximo de pelo qual a barra deverá ser alongada para dar a ela a deformação permanente desejada.
Passo 1
O que está acontecendo?
A barra é feita de dois segmentos:
- Um segmento de diâmetro e comprimento ;
- E outro de diâmetro e comprimento .
Além disso, ela possui um comportamento considerado elastoplástico com módulo de elasticidade e tensão de escoamento .
O que isso significa é que quando a tensão é atingida na barra, ela não é capaz de resistir qualquer tensão maior e passa a se deformar plasticamente/permanentemente.
No caso da nossa barra, a tensão vai ser atingida primeiro no trecho , que possui um diâmetro menor, e, consequentemente, uma área de seção transversal menor.
Isso significa que a variação de comprimento nesse trecho vai ser a soma:
- De uma variação de comprimento elástica até que a tensão de escoamento fosse atingida;
- Com uma deformação plástica/permanente que ocorre depois que a tensão de escoamento foi atingida.
Ou seja:
Já a variação de comprimento sofrida pelo trecho vai ser puramente elástica, uma vez que a tensão de escoamento nunca vai ser atingida nesse trecho.
(O trecho vai começar a se deformar livremente impedindo o aumento da carga e das tensões em toda a peça assim que a tensão nele alcançar .)
Então vamos ter que:
Então como o segmento não sofre deformação permanente, podemos dizer que toda a deformação permanente sofrida pela barra foi sofrida pelo segmento .
Ou seja:
E o que é que o exercício quer?
Primeiro, ele quer saber o valor máximo da força que foi aplicada nessa barra para que ela sofresse essa deformação plástica.
Como é o trecho que sofre a deformação plástica, o valor máximo de vai ser o valor para o qual a tensão normal média no trecho é igual à tensão de escoamento :
(Isso porque quando essa condição é atingida, a barra passa a se deformar livremente, impedindo que a força seja aumentada.)
Depois, ele quer saber a variação de comprimento máxima que foi sofrida pela barra para que ela tivesse a deformação permanente no trecho .
Aqui, podemos perceber que a variação de comprimento máxima da barra vai ser a soma das variações de comprimento de cada segmento:
Substituindo as expressões que encontramos para e , temos que:
Nessa expressão, sabemos que e que uma variação de comprimento pode ser calculada pela fórmula se ela for elástica.
Passo 2
Então para encontrar a força máxima na barra, vamos aplicar a condição de que ela acontece quando:
Aplicando a fórmula da tensão normal média para o trecho , temos que:
Como o único carregamento na barra é a tração , a força interna normal vai ser igual à , tanto no trecho quanto no trecho .
Além disso, o trecho possui uma seção transversal circular de diâmetro .
Então a área dessa seção transversal pode ser calculada usando a fórmula .
Aplicando tudo isso, a nossa expressão anterior fica assim:
Queremos encontrar a força máxima , então devemos isolá-la:
Finalmente, substituindo os valores:
- ;
- & ,
Encontramos que:
Como esse número é um pouco grande, podemos reescrevê-lo em na hora de darmos a nossa resposta para a primeira parte do exercício:
Passo 3
Agora, na segunda parte do exercício, queremos encontrar a variação de comprimento máxima que foi sofrida pela barra.
Como vimos no Passo 1, essa variação vai ser a soma:
- Das variações de comprimento elástica dos segmentos e ;
- Com a variação de comprimento permanente/plástica que foi sofrida pelo segmento .
Ou seja:
Nessa expressão, podemos desenvolver as variações elásticas usando a fórmula .
Aplicando essa fórmula para e para , vamos ter que:
Mais uma vez, como o único carregamento na barra é a tração , a força interna normal vai ser igual à , tanto no trecho quanto no trecho .
Além disso, como as áreas e são circulares, elas podem ser fornecidas em função de seus diâmetros e usando a fórmula .
Aplicando tudo isso, a expressão anterior fica assim:
Arrumando tudo, temos:
Colocando em evidência, temos:
Finalmente, substituindo os valores:
- ;
- ;
- e ;
- e ;
- & ,
Encontramos que:
Que é a nossa resposta para a segunda e última parte o exercício!