A figura mostra um processo cíclico, sofrido por moles de um gás ideal monoatômico, representado pelo plano , onde é a energia interna do sistema, e é a entropia. A respeito desse sistema, responda as seguintes questões:
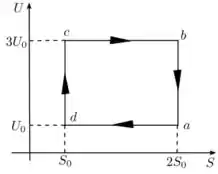
Identifique cada processo, isso é, se é isocórico, isotérmico, isobárico ou adiabático.
Calcule o trabalho realizado pelo sistema e o calor trocado por ele em cada etapa em termos de Indique explicitamente a convenção de sinais adotada.
Diga se o ciclo corresponde a uma máquina térmica ou a um refrigerador. Se for uma máquina, calcule a eficiência térmica, se for um refrigerador, calcule o coeficiente de desempenho.
O que podemos dizer desse ciclo em relação ao ciclo de Carnot? Qual é o mais eficiente?( Ou de melhor desempenho?).
Passo 1
Vamos lá:
Primeiro, de pra
Como nesse processo a energia interna é a mesma, a variação de energia interna é zero. Isso só acontece quando a temperatura é constante e, portanto, num processo isotérmico:
Isotérmico.
Nesse processo a variação de entropia é nula, então, só pode ser um processo adiabático:
adiabático.
Mesma coisa de antes, sem variação de energia interna, logo, isotérmico.
Isotérmico.
Sem variação de entropia, então, processo adiabático.
adiabático.
Passo 2
Por ser um processo isotérmico:
Usando a primeira lei:
Show?
Agora, lembrando da equação diferencial da entropia:
Como , se integrarmos nos dois lados:
Opa, encontramos uma equação para o trabalho. Só que não podemos usar esse
Lembra da equação da energia interna?:
Como o gás é monoatômico,
E:
Então:
Passo 3
Nesse caso, a variação de entropia é igual a zero por esse processo ser adiabático. Então, por ser adiabático, não há troca de calor:
Passo 4
:
Novamente, um processo isotérmico. Então vai ser bem parecido:
E:
Então:
Passo 5
:
Processo adiabático! Então:
Passo 6
Como descobrir se o ciclo representa uma máquina térmica ou um refrigerador? Bom, basta calcular o trabalho total.
Se for positivo, será uma máquina térmica, se for negativo, um refrigerador, já que a máquina térmica sempre “anda” no sentido horário e o refrigerador no sentido anti-horário. Assim:
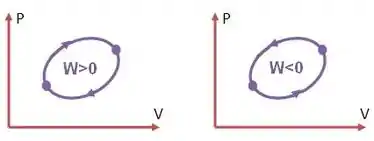
O trabalho total é a soma de todos os trabalhos e vale:
Como o trabalho total é positivo, o ciclo representa uma máquina térmica. Então o que precisamos calcular é a eficiência térmica:
Bom, o trabalho do ciclo nós já sabemos, mas quanto vale o calor absorvido da fonte quente?
Bom, temos achar em qual processo isso acontece. Temos 4 processos: 2 adiabáticos e 2 isotérmicos.
O calor não pode ter sido absorvido em nenhum dos dois adiabáticos, já que ali não há troca de calor, certo?
Então nos restam os processos isotérmicos. Em um dos processos isotérmicos, há um aumento de entropia, enquanto no outro há uma diminuição.
Entropia geralmente aumenta com o acréscimo de calor, não é mesmo? Já que a entropia mede a desordem de um sistema e acrescentar calor em um sistema não poderia deixar ele mais ordenado, só mais desordenado ( já que você tá enfiando mais energia nele).
Então o processo onde há ganho de calor é o processo . O calor dele a gente já calculou:
Então:
Passo 7
Vamos agora comparar a eficiência desse ciclo com a eficiência de um ciclo de Carnot operando entre as temperaturas extremas.
Bem, mas podemos resolver de outra forma.
Na nossa teoria, a gente viu que um ciclo de Carnot operando em um diagrama fica assim:
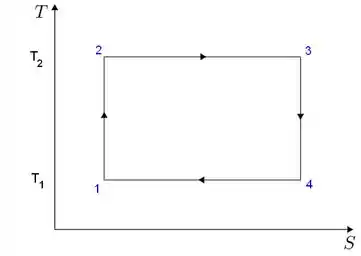
Beleza?
Bem, mas lembra que é função de Não só isso, é um função linear já que:
Então, isso quer dizer que um ciclo de Carnot operando num diagrama vai ter o mesmo formato que o formato acima.
Opa, mas é o formato que o enunciado nos dá:
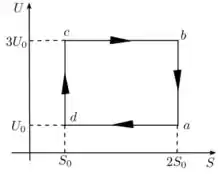
Conclusão: Esse é um ciclo de Carnot! Você poderia ter deduzido isso, também, vendo que um ciclo de Carnot sempre é formado por dois processos isotérmicos e dois processos adiabáticos.
Resposta: Mesma eficiência que um ciclo de Carnot.
Resposta
Isotérmico.
Adiabático.
Isotérmico.
Adiabático.
; ; ; ; ;
Máquina térmica.
Mesma eficiência de um ciclo de Carnot.