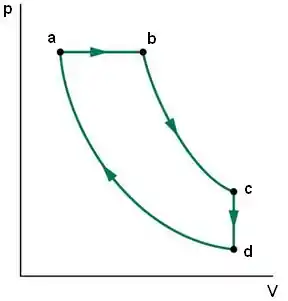
de um gás ideal é submetido a uma transformação cíclica reversível, representada no plano pelo diagrama abaixo:
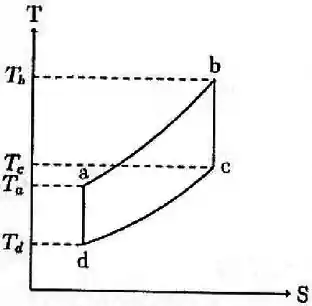
Na transformação , o gás sofre um aquecimento a pressão constante; em , um resfriamento adiabático; em , um resfriamento a volume constante; finalmente, em , um aquecimento adiabático.
Mostre, partindo de primeiros princípios, que
Dado que, no aquecimento a pressão constante, e, no resfriamento a volume constante, , calcule o trabalho realizado neste ciclo.
Desenhe o diagrama correspondente no plano , descrevendo cada processo, e calcule o trabalho, da maneira tradicional,APENAS no processo a pressão constante . Escreva o resultado em termos das temperaturas do sistema.
Passo 1
Resolvendo item
Como o ciclo é reversível, podemos calcular a variação de entropia do ciclo desta forma:
Na forma diferencial:
Substituindo na integral do ciclo:
Então, essa integral é o saldo de calor no ciclo.
Aplicando a Primeira Lei da Termodinâmica no ciclo:
Como a variação de energia interna só depende dos estados inicial e final, em um ciclo essa variação é zero.
Logo:
Então, se
Logo:
Passo 2
Resolvendo item
O trabalho realizado é dado por:
Ou seja:
Nos processos e , a área abaixo da curva é zero.
Então, precisamos calcular essa integral só nos processos e .
Passo 3
Calculando integral no processo :
Nesse processo, o enunciado nos disse que
Pois, nesse processo, a pressão é constante.
Substituindo na integral:
Logo:
Passo 4
Calculando integral no processo :
Nesse processo, o enunciado nos disse que
Pois, nesse processo, o volume é constante.
Substituindo na integral:
Logo:
Passo 5
Substituindo o que encontramos na integral do ciclo:
Logo, o trabalho realizado no ciclo é dado por:
Passo 6
Para desenhar o diagrama -, vamos ver quais curvas correspondem a cada processo:
: aquecimento a pressão constante
Nesse caso, como a pressão é constante, a curva é uma reta horizontal.
Como é um aquecimento, a direção é da esquerda para a direita, pois:
Como , então .
Pela equação do gás ideal a pressão constante:
Como a temperatura aumenta, o volume também aumenta. Por isso, o sentido da seta é da esquerda para a direita.
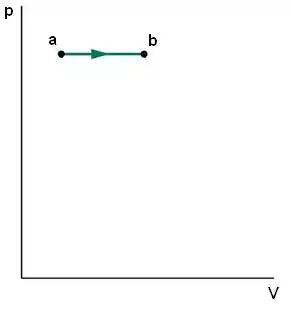
Passo 7
: resfriamento adiabático
A curva adiabática tem direção da esquerda para a direita, pois a temperatura diminui.
Sabemos que a curva adiabática é mais inclinada do que as isotermas:
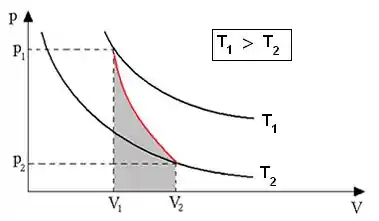
Então, nosso gráfico fica assim:
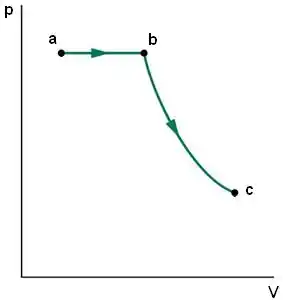
Passo 8
: resfriamento a volume constante
Nesse caso, a curva é uma reta vertical, pois o volume é constante.
Pela equação do gás ideal a volume constante:
Como a temperatura diminuiu, a pressão também diminui.
Então a direção é para baixo.
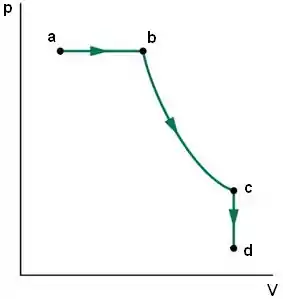
Passo 9
: aquecimento adiabático
Como é um aquecimento, a curva tem direção da direita para esquerda.
Pra fechar o ciclo, só poderia ser assim mesmo.
Então o gráfico fica assim:
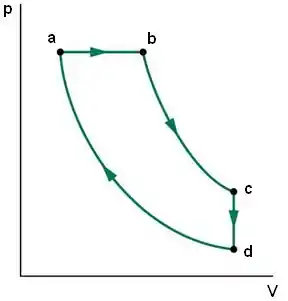
Passo 10
Eu imagino que a “maneira tradicional” de calcular trabalho é pela integral:
Ou seja, a área sobre a curva no diagrama -.
No processo isobárico , temos .
Logo:
O problema nos pede que o trabalho seja colocado em termos das temperaturas.
Colocando a equação do gás ideal nos pontos e :
Subtraindo a segunda da primeira:
Como :
Resposta