Seja o ciclo abaixo, realizado por n moles de um gás ideal, no plano . Considere conhecidas as temperaturas e e a diferença de entropia .
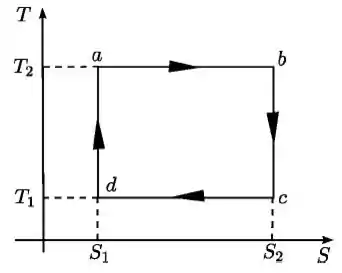
Calcule o trabalho total do ciclo em função de . Este ciclo representa uma máquina ou um refrigerador? Justifique.
Passo 1
Bom, olha só que malandragem vamos usar agora pra resolver essa questão de um jeito tranquilinho....Se liga na marotagem...
Para um ciclo, temos que a variação de energia interna é nula. Assim:
Então basta a gente calcular o calor total do ciclo! Olha só! Simples assim! 
Já que:
Passo 2
Bom, como acabamos de calcular o trabalho para o ciclo e vimos que se trata de um valor positivo, chegamos à conclusão de que se trata de uma máquina térmica.
Resposta
Se trata, portanto, de uma Máquina Térmica
Exercícios de Livros Relacionados
Suponha que 2 m o l s de um gás diatômico ideal sejam submetidos reversivelmente ao ciclo mostrado no diagrama T - S na figura abaixo, onde S 1 = 6 J / K e S 2 = 8 J / K . As moléculas não giram nem o
Um fluido é submetido a um ciclo reversível. Se o ciclo é representado por um diagrama no plano ( T , S ) , onde S é a entropia do fluido, (a) Mostre que o trabalho associado ao ciclo é dado por W = ⨕
a)Faça um gráfico do ciclo de Carnot, indicando a entropia no eixo horizontal e a temperatura em Kelvin no eixo vertical. Trata-se de um diagrama temperatura -entropia, ou diagrama T S . b) Mostre que